
如图,一个4×2的矩形可以用3种不同的方式分割成2或5或8个小正方形.
(1)一个3×2的矩形用不同的方式分割后,小正方形的个数可以是 ;
一个5×2的矩形用不同的方式分割后,小正方形的个数可以是 ;
(2)一个n×2的矩形用不同的方式分割后,小正方形的个数最少是___________.(直接填写结果).
(1)3或6;4、7或10;(2)当n为偶数时,最少 个,当n为奇数时,最少
个,当n为奇数时,最少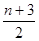 个
个
解析试题分析:(1)一个3×2的矩形可以是1个2×2和2个1×1或6个1×1的.
(2)一个5×2的矩形可以是2个2×2和2个1×1或1个2×2和6个1×1或10个1×1的.
(3)一个n×2的矩形用不同的方式分割后,小正方形都是1×1的小正方形的个数最多,分奇偶性讨论小正方形的个数最少的情况;
(1)一个3×2的矩形用不同的方式分割后,小正方形的个数可以是3或6;
(2)一个5×2的矩形用不同的方式分割后,小正方形的个数可以是4或7或10;
(3)当n为偶数时,最少 个,当n为奇数时,最少
个,当n为奇数时,最少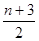 个.
个.
考点:找规律-图形的变化
点评:解题的关键是通过归纳与总结,得到其中的规律,注意正方形可以是1×1的或2×2的或3×3的.


科目:初中数学 来源: 题型:
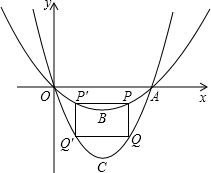 如图,抛物线y1与y2都与x轴交于点O(0,0)和点A,y1的顶点是B(2,-1),y2的顶点是C(2,-3),P是y1上的一个动点,过P作y轴的平行线交y2于点Q,分别过P,Q作x轴的平行线,分别交y1,y2于点P′,Q′,连接P′Q′.
如图,抛物线y1与y2都与x轴交于点O(0,0)和点A,y1的顶点是B(2,-1),y2的顶点是C(2,-3),P是y1上的一个动点,过P作y轴的平行线交y2于点Q,分别过P,Q作x轴的平行线,分别交y1,y2于点P′,Q′,连接P′Q′.查看答案和解析>>
科目:初中数学 来源: 题型:
如图,正方形ABCD和正方形EFGH的边长分别为2![]() 和
和![]() ,对角线BD,FH都在直线L上,O1,O2分别是正方形的中心,线段O1O2的长叫做两个正方形的中心矩.当中心O2在直线L上平移时,正方形EFGH也随着平移,在平移时正方形EFGH的形状,大小没有改变.
,对角线BD,FH都在直线L上,O1,O2分别是正方形的中心,线段O1O2的长叫做两个正方形的中心矩.当中心O2在直线L上平移时,正方形EFGH也随着平移,在平移时正方形EFGH的形状,大小没有改变.
(1)计算:O1D=_______,O2F=_______.
(2)当中心O2在直线L上平移到两个正方形只有一个公共点时,中心距O1O2=_____.
(3)随着中心O2在直线L上的平移,两个正方形的公共点的个数还有哪些变化?并求出相对应的中心距的值或取值范围(不必写出计算过程).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com