
 已知:如图,在平面直角坐标系中,正方形ABCD的边长为8.求出AC和BD的长度,并直接写出它的四个顶点A、B、C、D的坐标.
已知:如图,在平面直角坐标系中,正方形ABCD的边长为8.求出AC和BD的长度,并直接写出它的四个顶点A、B、C、D的坐标. 分析 根据题意和图形可知,∠AOD=90°,OA=OC=OB=OD,BD=AC,AD=8,然后根据勾股定理可求得OA、OD的长,从而得到AC和BD的长度,从而写出它的四个顶点A、B、C、D的坐标.
解答 解:∵在平面直角坐标系中,正方形ABCD的边长为8.
∴∠AOD=90°,OA=OC=OB=OD,BD=AC,AD=8.
∴OA2+OD2=82.
解得,OA=OD=$4\sqrt{2}$.
∴AC=BD=$8\sqrt{2}$.
∴点A的坐标为:(-$2\sqrt{2}$,0),B的坐标为:(0,$-2\sqrt{2}$)C的坐标为:($2\sqrt{2}$,0),D点的坐标为:(0,2$\sqrt{2}$).
点评 本题考查正方形与坐标系的相关知识,关键是找出其中的对应量.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:解答题
 某工程队准备开挖一条隧道,为了缩短工期,必须在山的两侧同时开挖,为了确保两侧开挖的隧道在同一条直线上,测量人员在如图所示的同一高度定出了两个开挖点P和Q,然后在左边定出开挖的方向线AP,为了准确定出右边开挖的方向线BQ,测量人员取一个可以同时看到点A,P,Q的点O,测得∠A=28°,∠AOC=100°,那么∠QBO应等于多少度才能确保BQ与AP在同一条直线上?
某工程队准备开挖一条隧道,为了缩短工期,必须在山的两侧同时开挖,为了确保两侧开挖的隧道在同一条直线上,测量人员在如图所示的同一高度定出了两个开挖点P和Q,然后在左边定出开挖的方向线AP,为了准确定出右边开挖的方向线BQ,测量人员取一个可以同时看到点A,P,Q的点O,测得∠A=28°,∠AOC=100°,那么∠QBO应等于多少度才能确保BQ与AP在同一条直线上?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
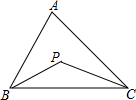 如图,在三角形ABC中,∠ABC与∠ACB的平分线交于点P,设∠A=x°,∠BPC=y°,当∠A变化时,求y与x之间的函数关系式.并判断y是不是x的一次函数.
如图,在三角形ABC中,∠ABC与∠ACB的平分线交于点P,设∠A=x°,∠BPC=y°,当∠A变化时,求y与x之间的函数关系式.并判断y是不是x的一次函数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{8}{27}$ | D. | $\frac{2}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com