
【题目】已知![]() ∥
∥![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的两点,点
上的两点,点![]() 在
在![]() 、
、![]() 之间,连接
之间,连接![]() 、
、![]() .
.
(1)如图①,若![]() ,求
,求![]() 的度数;
的度数;
(2)如图②,若点![]() 是
是![]() 下方一点,
下方一点,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,已知
,已知![]() ,求
,求![]() 的度数;
的度数;
(3)如图③,若点![]() 是
是![]() 上方一点,连接
上方一点,连接![]() 、
、![]() ,且
,且![]() 的延长线
的延长线![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() ,求
,求![]() 的度数.
的度数.



【答案】(1)90°;(2)90°;(3)50°
【解析】
(1)过G作GH∥AB,依据两直线平行,内错角相等,即可得到∠AMG+∠CNG的度数;
(2)过G作GK∥AB,过点P作PQ∥AB,设∠GND=α,利用平行线的性质以及角平分线的定义,求得∠MGN=30°+α,∠MPN=60°-α,即可得到∠MGN+∠MPN=30°+α+60°-α=90°;
(3)过G作GK∥AB,过E作ET∥AB,设∠AMF=x,∠GND=y,利用平行线的性质以及角平分线的定义,可得∠MEN=∠TEN-∠TEM=90°-![]() y-2x,∠MGN=x+y,再根据2∠MEN+∠G=105°,即可得到2(90°-
y-2x,∠MGN=x+y,再根据2∠MEN+∠G=105°,即可得到2(90°-![]() y-2x)+x+y=105°,求得x=25°,即可得出∠AME=2x=50°.
y-2x)+x+y=105°,求得x=25°,即可得出∠AME=2x=50°.
解:(1)如图1,过G作GH∥AB,

∵AB∥CD,
∴GH∥AB∥CD,
∴∠AMG=∠HGM,∠CNG=∠HGN,
∵MG⊥NG,
∴∠MGN=∠MGH+∠NGH=∠AMG+∠CNG=90°;
(2)如图2,过G作GK∥AB,过点P作PQ∥AB,设∠GND=α,

∵GK∥AB,AB∥CD,
∴GK∥CD,
∴∠KGN=∠GND=α,
∵GK∥AB,∠BMG=30°,
∴∠MGK=∠BMG=30°,
∵MG平分∠BMP,ND平分∠GNP,
∴∠GMP=∠BMG=30°,
∴∠BMP=60°,
∵PQ∥AB,
∴∠MPQ=∠BMP=60°,
∵ND平分∠GNP,
∴∠DNP=∠GND=α,
∵AB∥CD,
∴PQ∥CD,
∴∠QPN=∠DNP=α,
∴∠MGN=30°+α,∠MPN=60°-α,
∴∠MGN+∠MPN=30°+α+60°-α=90°;
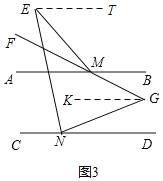
(3)如图3,过G作GK∥AB,过E作ET∥AB,设∠AMF=x,∠GND=y,
∵AB,FG交于M,MF平分∠AME,
∴∠FME=∠FMA=∠BMG=x,
∴∠AME=2x,
∵GK∥AB,
∴∠MGK=∠BMG=x,
∵ET∥AB,
∴∠TEM=∠EMA=2x,
∵CD∥AB∥KG,
∴GK∥CD,
∴∠KGN=∠GND=y,
∴∠MGN=x+y,
∵∠CND=180°,NE平分∠CNG,
∴∠CNG=180°-y,∠CNE=![]() ∠CNG=90°-
∠CNG=90°-![]() y,
y,
∵ET∥AB∥CD,
∴ET∥CD,
∴∠TEN=∠CNE=90°-![]() y,
y,
∴∠MEN=∠TEN-∠TEM=90°-![]() y-2x,∠MGN=x+y,
y-2x,∠MGN=x+y,
∵2∠MEN+∠G=105°,
∴2(90°-![]() y-2x)+x+y=105°,
y-2x)+x+y=105°,
∴x=25°,
∴∠AME=2x=50°.


科目:初中数学 来源: 题型:
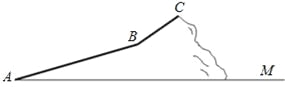
【题目】今年“五一“假期.某数学活动小组组织一次登山活动.他们从山脚下A点出发沿斜坡AB到达B点.再从B点沿斜坡BC到达山顶C点,路线如图所示.斜坡AB的长为1040米,斜坡BC的长为400米,在C点测得B点的俯角为30°.已知A点海拔121米.C点海拔721米.
(1)求B点的海拔;
(2)求斜坡AB的坡度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数![]() 的图象经过
的图象经过![]() ,
,![]() ,其中
,其中![]() ,过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,连结AD,DC,CB,AC与BD相交于点E.
,过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,连结AD,DC,CB,AC与BD相交于点E.

(1)若![]() 的面积为4,求点B的坐标;
的面积为4,求点B的坐标;
(2)四边形ABCD能否成为平行四边形,若能,求点B的坐标,若不能说明理由;
(3)当![]() 时,求证:四边形ABCD是等腰梯形.
时,求证:四边形ABCD是等腰梯形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 、
、![]() 三点在数轴上,点
三点在数轴上,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 为线段
为线段![]() 的中点.动点
的中点.动点![]() 在数轴上,且点
在数轴上,且点![]() 表示的数为
表示的数为![]() .
.

(1)求点![]() 表示的数;
表示的数;
(2)点![]() 从点
从点![]() 出发,向终点
出发,向终点![]() 运动.设
运动.设![]() 中点为
中点为![]() .请用含
.请用含![]() 的整式表示线段
的整式表示线段![]() 的长.
的长.
(3)在(2)的条件下,当![]() 为何值时,
为何值时,![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E,连接AG.
(1)求证:AG=CG;
(2)求证:AG2=GE·GF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“格子乘法”作为两个数相乘的一种计算方法最早在15世纪由意大利数学家帕乔利提出,在明代的《算法统宗》一书中被称为“铺地锦”.如图1,计算![]() ,将乘数47计入上行,乘数51计入右行,然后以乘数47的每位数字乘以乘数51的每位数字,将结果计入相应的格子中,最后按斜行加起来,得2397.
,将乘数47计入上行,乘数51计入右行,然后以乘数47的每位数字乘以乘数51的每位数字,将结果计入相应的格子中,最后按斜行加起来,得2397.

(1)如图2,用“格子乘法”表示![]() ,则
,则![]() 的值为__________.
的值为__________.
(2)如图3,用“格子乘法”表示两个两位数相乘,则![]() 的值为___________.
的值为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线C1:y=x2﹣1(﹣1≤x≤1)与x轴交于A、B两点,抛物线C2与抛物线C1关于点A中心对称,抛物线C3与抛物线C1关于点B中心对称.若直线y=﹣x+b与由C1、C2、C3组成的图形恰好有2个公共点,则b的取值或取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】浠水县商场某柜台销售每台进价分别为160元、120元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 4台 | 1200元 |
第二周 | 5台 | 6台 | 1900元 |
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,商场销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com