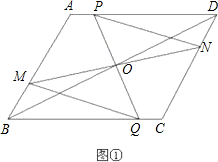
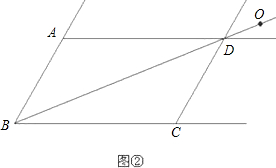
解:(1)利用平行四边形的性质:对边平行且相等,
得出图1、图2,3中顶点C的坐标分别是:(5,2)、(e+c,d),(c+e-a,d).
故答案为:(5,2)、(e+c,d),(c+e-a,d).
(2)分别过点A,B,C,D作x轴的垂线,垂足分别为A
1,B
1,C
1,D
1,
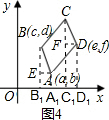
分别过A,D作AE⊥BB
1于E,DF⊥CC
1于点F.
在平行四边形ABCD中,CD=BA,
又∵BB
1∥CC
1,
∴∠EBA+∠ABC+∠BCF=∠ABC+∠BCF+∠FCD=180度.
∴∠EBA=∠FCD.
又∵∠BEA=∠CFD=90°,
∴△BEA≌△CFD.
∴AE=DF=a-c,BE=CF=d-b.
设C(x,y).
由e-x=a-c,得x=e+c-a.
由y-f=d-b,得y=f+d-b.
∴C(e+c-a,f+d-b).
(3)m=c+e-a,n=d+f-b或m+a=c+e,n+b=d+f.
分析:(1)根据平行四边形的性质:对边平行且相等,得出图2,3中顶点C的坐标分别是(e+c,d),(c+e-a,d);
(2)分别过点A,B,C,D作x轴的垂线,垂足分别为A
1,B
1,C
1,D
1,分别过A,D作AE⊥BB
1于E,DF⊥CC
1于点F.在平行四边形ABCD中,CD=BA,根据内角和定理,又∵BB
1∥CC
1,可推出∠EBA=∠FCD,△BEA≌△CFD.依题意得出AF=DF=a-c,BE=CF=d-b.设C(x,y).由e-x=a-c,得x=e+c-a.由y-f=d-b,得y=f+d-b.继而推出点C的坐标.
(3)在平行四边形ABCD中,CD=BA,同理证明△BEA≌△CFD(同(2)证明).然后推出AF=DF=a-c,BE=CF=d-b.又已知C点的坐标为(m,n),e-m=a-c,故m=e+c-a.由n-f=d-b,得出n=f+d-b.
点评:此题主要考查了平行四边形的性质,平面直角坐标系内的坐标,平行线的性质等知识.理解平行四边形的特点结合平面直角坐标系是解决本题的关键.





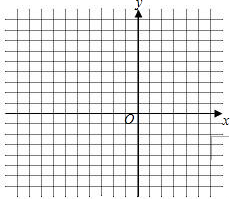 在平面直角坐标系中
在平面直角坐标系中 如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫格点,请在给定的网格中按要求画图:
如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫格点,请在给定的网格中按要求画图: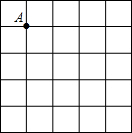 (1)从点A出发画一条线段AB,使它的另一端点B在格点(即小正方形的顶点)上,且长度为
(1)从点A出发画一条线段AB,使它的另一端点B在格点(即小正方形的顶点)上,且长度为