
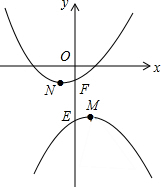
 如图,抛物线y1=-ax2+2ax-a-3(a>0)和y2=a(x+1)2-1(a>0)的顶点分别为M、N,与y轴分别交于E、F.
如图,抛物线y1=-ax2+2ax-a-3(a>0)和y2=a(x+1)2-1(a>0)的顶点分别为M、N,与y轴分别交于E、F.分析 (1)①利用配方法得到y1=-a(x-1)2-3,可得到函数的最大值;②依据二次函数的性质判断出每个二次函数y随x的增大而增大的范围,然后再求得其公共部分即可;
(2)由函数解析式可知:N(-1,-1),M(1,-3),依据两点间的距离公式可求得MN=2$\sqrt{2}$,然后再求得点F、E的坐标,然后依据EF=MN可求得a的值,作NC⊥y轴于C,MD⊥y轴于D,然后证明△NCF≌MDE,可得到NF=EM,NF‖EM
则四边形EMFN是平行四边形,然后由NM=EF可得到四边形EMFN的形状;
(3)依据两点间的距离公式可得到AN2=m2+2m+2,AM2=m2-2m+10,MN2=8,然后分为AN=AM,AN=MN,AM=MN,三种情况求得m的值,从而得到方程的一个解,然后利用抛物线的对称性可求得方程的另一个解.
解答 解:(1)①y1=-ax2+2ax-a-3=-a(x2-2x+1)-3=-a(x-1)2-3,
∴函数y1=-ax2+2ax-a-3(a>0)的最大值是-3.
故答案为:-3.
②∵y1=-a(x-1)2-3,-a<0,
∴当x≤1时,y随x的增大而增大.
∵y2=a(x+1)2-1(a>0),
∴当x≥-1时,y随x的增大而增大.
∴当-1≤x≤1时,y1、y2的值都随x的增大而增大.
(2)∵y1=-a(x-1)2-3,y2=a(x+1)2-1,
∴N(-1,-1),M(1,-3).
由两点间的距离公式可知:MN=2$\sqrt{2}$.
令x=0得:y1=-a-3,y2=a-1.
∴F(0,a-1),E(0,-a-3).
∴EF=2a+2.
∵EF=MN,
∴2a+2=2$\sqrt{2}$,解得:a=$\sqrt{2}$-1.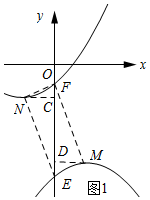
作NC⊥y轴于C,MD⊥y轴于D
∴NC=1,FC=a,MD=1,DE=a
∵在Rt△CNF和Rt△MDE中,$\left\{\begin{array}{l}{CF=DE}\\{∠NCF=∠MDE}\\{CN=MD}\end{array}\right.$,
∴△NCF≌MDE.
∴NF=EM,∠NFC=∠DEM
∴NF‖EM
∴四边形EMFN是平行四边形
又∵NM=EF
∴四边形EMFN是矩形.
(3)∵A(m,0)M(1,-3)N(-1,-1),
∴AN2=m2+2m+2,AM2=m2-2m+10,MN2=8.
①若AN=AM,则m2+2m+2=m2-2m+10,解得:m=2,
∴方程a(x+1)2-1=0的一个解为x=2,
根据抛物线对称性,可知方程的另一个解为x=-4.
②若AN=MN,则m2+2m+2=8,解得:m=-1+$\sqrt{7}$或m=-1-$\sqrt{7}$(舍去),
所以方程a(x+1)2-1=0的一个解为x=-1+$\sqrt{7}$,
根据抛物线对称性,可知方程的另一个解为x=-1-$\sqrt{7}$.
③若AM=MN,所以m2-2m+10=8,
此方程无解,所以此种情况不成立
综上所述当△AMN为等腰三角形时,方程a(x+1)2-1=0的解为x1=2,x2=-4或x1=-1$+\sqrt{7}$或x2=-1-$\sqrt{7}$.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了二次函数的性质、全等三角形的性质和判定、等腰三角形的定义、矩形的判定,证得△NCF≌MDE是解答问题(2)的关键,分类讨论是解答问题(3)的关键.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)化简:(x+1)2-x(2-x)
(1)化简:(x+1)2-x(2-x)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,射线BC交⊙O于点D,E是劣弧AD上一点,且$\widehat{AE}=\widehat{DE}$,过点E作EF⊥BC于点F,延长FE和BA的延长线交与点G.
如图,AB是⊙O的直径,射线BC交⊙O于点D,E是劣弧AD上一点,且$\widehat{AE}=\widehat{DE}$,过点E作EF⊥BC于点F,延长FE和BA的延长线交与点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
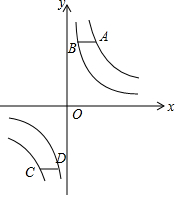 如图,已知点A、C在反比例函数y=$\frac{4}{x}$的图象上,点B、D在反比例函数y=$\frac{b}{x}$(0<b<4)的图象上,AB∥CD∥x轴,AB、CD在x轴的两侧,A、C的纵坐标分别为m(m>0)、n(n<0).
如图,已知点A、C在反比例函数y=$\frac{4}{x}$的图象上,点B、D在反比例函数y=$\frac{b}{x}$(0<b<4)的图象上,AB∥CD∥x轴,AB、CD在x轴的两侧,A、C的纵坐标分别为m(m>0)、n(n<0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,半径为2的正六边形ABCDEF的中心在坐标原点O,点P从点B出发,沿正六边形的边按顺时针方向以每秒2个单位长度的速度运动,则第2017秒时,点P的坐标是( )
如图,半径为2的正六边形ABCDEF的中心在坐标原点O,点P从点B出发,沿正六边形的边按顺时针方向以每秒2个单位长度的速度运动,则第2017秒时,点P的坐标是( )| A. | (1,$\sqrt{3}$) | B. | (-1,-$\sqrt{3}$) | C. | (1,-$\sqrt{3}$) | D. | (-1,$\sqrt{3}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com