【题目】若等腰△ABC的周长为20，AB=8，则该等腰三角形的腰长为（ ）．
A.8B.6C.4D.8或6
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，点O为坐标原点，抛物线
经过点M（1，3）和N（3，5）
（1）试判断该抛物线与x轴交点的情况；
（2）平移这条抛物线，使平移后的抛物线经过点A（﹣2，0），且与y轴交于点B，同时满足以A、O、B为顶点的三角形是等腰直角三角形，请你写出平移过程，并说明理由．
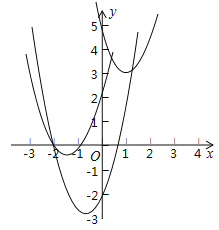
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知P1（﹣2，y1），P2（1，y2）是函数y＝﹣2x+1图象上的两个点，则y1与y2的大小关系是（ ）
A.y1＞y2B.y1＜y2C.y1＝y2D.无法确定
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，面积为6的平行四边形纸片ABCD中，AB=3，∠BAD=45°，按下列步骤进行裁剪和拼图．
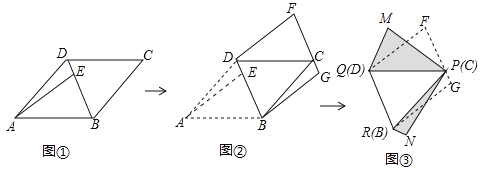
第一步：如图①，将平行四边形纸片沿对角线BD剪开，得到△ABD和△BCD纸片，再将△ABD纸片沿AE剪开（E为BD上任意一点），得到△ABE和△ADE纸片；
第二步：如图②，将△ABE纸片平移至△DCF处，将△ADE纸片平移至△BCG处；
第三步：如图③，将△DCF纸片翻转过来使其背面朝上置于△PQM处（边PQ与DC重合，△PQM和△DCF在DC同侧），将△BCG纸片翻转过来使其背面朝上置于△PRN处，（边PR与BC重合，△PRN和△BCG在BC同侧）．则由纸片拼成的五边形PMQRN中，对角线MN长度的最小值为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】(1) 定义：直角三角形两直角边的平方和等于斜边的平方．如：直角三角形的直角边分别为3、4，则斜边的平方=32+42=25.已知：Rt△ABC中，∠C=90°，AC=8，AB=10,直接写出BC2=__________________．
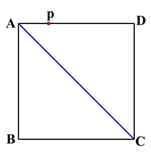
（2）应用：已知正方形ABCD的边长为4，点P为AD边上的一点，AP= 
,请利用“两点之间线段最短”这一原理，在线段AC上画出一点M，使MP+MD最小，并直接写出最小值的平方为_____________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】现代互联网技术的广泛应用，催生了快递行业的高速发展．小明计划给朋友快递一部分物品，经了解有甲、乙两家快递公司比较合适．甲公司表示：快递物品不超过1千克的，按每千克22元收费；超过1千克，超过的部分按每千克15元收费．乙公司表示：按每千克16元收费，另加包装费3元．设小明快递物品x千克．
（1）请分别写出甲、乙两家快递公司快递该物品的费用y（元）与x（千克）之间的函数关系式；
（2）小明选择哪家快递公司更省钱？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知在纸面上有一数轴(如图所示)，
操作一：(1)折叠纸面,使1表示的点与1表示的点重合，回答一下问题：
①2表示的点与______表示的点重合；②π表示的点与______表示的点重合。
操作二：(2)折叠纸面,使1表示的点与3表示的点重合，回答以下问题：
①5表示的点与数_____表示的点重合；②
表示的点与数_____表示的点重合
操作三：（3）已知在数轴上点A表示的数是a，点A移动5个单位，此时点A表示的数和a是互为相反数，求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
