
| x |
| -x |
| x |
| -x |
|
| x2-1 |
| 1-x2 |
| x-2 |
| 2-x |
| x2-1 |
| 1-x2 |
|
| x-2 |
| 2-x |
|
| 1 |
| 8 |



| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєФД¶БАнЅв
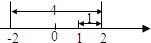 28Ўў
28Ўў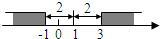 ФД¶БПВБРІДБПЈє
ФД¶БПВБРІДБПЈєІйїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєФД¶БАнЅв
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєЅвґрМв
 УРТвТеЈ¬ФтxЎЭ0Ј»КЅЧУ
УРТвТеЈ¬ФтxЎЭ0Ј»КЅЧУ УРТвТеЈ¬ФтxЎЬ0Ј»ИфКЅЧУ
УРТвТеЈ¬ФтxЎЬ0Ј»ИфКЅЧУ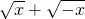 УРТвТеЈ¬ЗуxµДИЎЦµ·¶О§Ј»ХвёцОКМвїЙТФЧЄ»ЇОЄІ»µИКЅЧйАґЅвѕцЈ¬јґЗу№ШУЪxµДІ»µИКЅЧй
УРТвТеЈ¬ЗуxµДИЎЦµ·¶О§Ј»ХвёцОКМвїЙТФЧЄ»ЇОЄІ»µИКЅЧйАґЅвѕцЈ¬јґЗу№ШУЪxµДІ»µИКЅЧй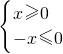 µДЅвјЇЈ¬ЅвХвёцІ»µИКЅЧйµГx=0Ј®ЗлДгФЛУГЙПКцµДКэС§·Ѕ·ЁЅвѕцПВБРОКМвЈє
µДЅвјЇЈ¬ЅвХвёцІ»µИКЅЧйµГx=0Ј®ЗлДгФЛУГЙПКцµДКэС§·Ѕ·ЁЅвѕцПВБРОКМвЈє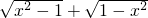 УРТвТеЈ¬ЗуxµДИЎЦµ·¶О§Ј»
УРТвТеЈ¬ЗуxµДИЎЦµ·¶О§Ј»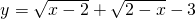 Ј¬ЗуxyµДЦµЈ®
Ј¬ЗуxyµДЦµЈ®Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈєІ»Пк МвРНЈєЅвґрМв
| x |
| -x |
| x |
| -x |
|
| x2-1 |
| 1-x2 |
| x-2 |
| 2-x |
Ійїґґр°ёєНЅвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com