
分析 先将二次根式都化成最简二次根式后再合并;有括号的要先去括号.
解答 解:(1)9$\sqrt{3}$+7$\sqrt{12}$-5$\sqrt{48}$,
=9$\sqrt{3}$+7×2$\sqrt{3}$-5×4$\sqrt{3}$,
=9$\sqrt{3}$+14$\sqrt{3}$-20$\sqrt{3}$,
=(9+14-20)$\sqrt{3}$,
=3$\sqrt{3}$;
(2)$\sqrt{24}$+$\sqrt{12}$-$\sqrt{6}$,
=2$\sqrt{6}$+2$\sqrt{3}$-$\sqrt{6}$,
=$\sqrt{6}$+2$\sqrt{3}$;
(3)$\sqrt{18}$+3$\sqrt{8}$+3$\sqrt{22}$-$\sqrt{50}$,
=3$\sqrt{2}$+3×$2\sqrt{2}$+3$\sqrt{22}$-5$\sqrt{2}$,
=3$\sqrt{2}$+6$\sqrt{2}$+3$\sqrt{22}$-5$\sqrt{2}$,
=4$\sqrt{2}$+3$\sqrt{22}$;
(4)($\sqrt{12}$-4$\sqrt{\frac{1}{8}}$)-(3$\sqrt{\frac{1}{3}}$-4$\sqrt{0.5}$),
=2$\sqrt{3}$-4×$\frac{\sqrt{2}}{4}$-3×$\frac{\sqrt{3}}{3}$+4×$\frac{\sqrt{2}}{2}$,
=2$\sqrt{3}$-$\sqrt{2}$-$\sqrt{3}$+2$\sqrt{2}$,
=$\sqrt{3}$+$\sqrt{2}$;
(5)$\sqrt{27}$-$\frac{1}{3}$$\sqrt{18}$-$\sqrt{12}$,
=3$\sqrt{3}$-$\frac{1}{3}$×3$\sqrt{2}$-2$\sqrt{3}$,
=$\sqrt{3}$-$\sqrt{2}$;
(6)$\frac{1}{2}$($\sqrt{2}$+$\sqrt{3}$)-$\frac{3}{4}$($\sqrt{2}$-$\sqrt{27}$),
=$\frac{1}{2}\sqrt{2}$+$\frac{1}{2}\sqrt{3}$-$\frac{3}{4}\sqrt{2}$+$\frac{3}{4}×3\sqrt{3}$,
=($\frac{1}{2}$-$\frac{3}{4}$)$\sqrt{2}$+($\frac{1}{2}$+$\frac{9}{4}$)$\sqrt{3}$,
=-$\frac{1}{4}$$\sqrt{2}$+$\frac{11}{4}$$\sqrt{3}$.
点评 本题是二次根式的加减法,进行计算时,二次根式要先化成最简二次根式,如果被开方数相同则可以进行合并.合并时,只合并根式外的因式,即系数相加减,被开方数和根指数不变.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:解答题
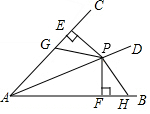 如图,已知:P是∠AOB平分线上一点,PE⊥OA,PF⊥OB,垂足分别是E,F,G,H分别是OA,OB上两点,且PG=PH,求证:EG=FH.
如图,已知:P是∠AOB平分线上一点,PE⊥OA,PF⊥OB,垂足分别是E,F,G,H分别是OA,OB上两点,且PG=PH,求证:EG=FH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD和GBHD都是平行四边形,G,H分别在AB,CD边上,连接AC分别交DG,BH于点F,M,过F作FE∥AD交CD于E.若$\frac{DE}{EC}$=$\frac{2}{5}$.
如图,四边形ABCD和GBHD都是平行四边形,G,H分别在AB,CD边上,连接AC分别交DG,BH于点F,M,过F作FE∥AD交CD于E.若$\frac{DE}{EC}$=$\frac{2}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com