

分析 (1)根据同弧所对的圆周角相等,推出∠BDC=∠BAC=60°,∠ADC=∠ACB=60°即可解决问题.
(2)如图2中,在BD上截取DH=DC,作EN⊥AD,EM⊥CD垂足分别为N、M.由△ACD≌△BCH推出BD=DA+DC,结合条件推出AD=2DC,再根据$\frac{{S}_{△ADE}}{{S}_{△EDC}}$=$\frac{AE}{EC}$=$\frac{\frac{1}{2}•AD•EN}{\frac{1}{2}•CD•EM}$=$\frac{2}{1}$,即可证明.
(3)如图3中,连接AO,由此AO交BC于M,连接OE,作EN⊥BC于N,设OE=x.用x表示BN、EN,在Rt△EBN中,利用勾股定理列出方程即可.
解答 (1)证明:如图1中,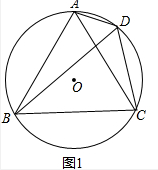
∵△ABC是等边三角形,
∴∠BAC=∠ACB=60°,
∵∠BDC=∠BAC,∠ADC=∠ACB,
∴∠ADB=∠BDC=60°.
(2)如图2中,在BD上截取DH=DC,作EN⊥AD,EM⊥CD垂足分别为N、M.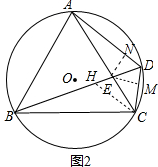
∵∠HDC=60°,DH=DC,
∴△DHC是等边三角形,
∴HC=DC,∠CHD=60°,
∴∠BCA=∠HCD=60°,
∴∠BCH=∠ACD,
在△BCH和△ACD中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCH}\\{CD=CH}\end{array}\right.$,
∴△ACD≌△BCH,
∴BH=AD,
∴BD=BH+HD=AD+CD.
∵BD=3CD,
∴3CD=AD+CD,
∴AD=2CD,
∵∠ADB=∠BDC,EN⊥DA,EM⊥DC,
∴EN=EM,
∵$\frac{{S}_{△ADE}}{{S}_{△EDC}}$=$\frac{AE}{EC}$=$\frac{\frac{1}{2}•AD•EN}{\frac{1}{2}•CD•EM}$=$\frac{2}{1}$,
∴AE=2CE.
(3)如图3中,连接AO,由此AO交BC于M,连接OE,作EN⊥BC于N,设OE=x.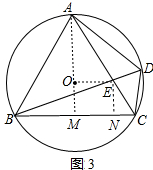
∵O是等边三角形的外心,
∴OA=2OM,∵AE=2EC,
∴$\frac{OA}{OM}$=$\frac{AE}{EC}$,
∴OE∥CM,
∵AM⊥BC,
∴AO⊥OE,
∵∠OAE=$\frac{1}{2}$∠BAC=30°,
∴AE=2x,EC=x,CN=$\frac{1}{2}$x,BN=$\frac{5}{2}$x,EN=$\frac{\sqrt{3}}{2}$x
在Rt△BNE中,∵BE2=BN2+EN2,
∴142=($\frac{5}{2}x$)2+($\frac{\sqrt{3}}{2}$x)2,
∴x2=28,
∵x>0,
∴x=2$\sqrt{7}$.
∴OE=2$\sqrt{7}$.
点评 本题考查圆的综合题、全等三角形的判定和性质、平行线的判定.勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会把问题转化为方程去思考,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
 如图,在坐标平面内,依次作点P(-1,2)关于直线y=x的对称点P1,P1关于x轴的对称点P2,P2关于y轴的对称点P3;P3关于直线y=x的对称点P4,P4关于x轴的对称点P5,P5关于y轴的对称点P6,…,按照上述的变换继续作对称点Pn,Pn+1,Pn+2,当n=2016时,点Pn+2的坐标为(2,1).
如图,在坐标平面内,依次作点P(-1,2)关于直线y=x的对称点P1,P1关于x轴的对称点P2,P2关于y轴的对称点P3;P3关于直线y=x的对称点P4,P4关于x轴的对称点P5,P5关于y轴的对称点P6,…,按照上述的变换继续作对称点Pn,Pn+1,Pn+2,当n=2016时,点Pn+2的坐标为(2,1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,D、E分别是AB、AC上的点,DC、BE交于F,则下列结论一定正确的是( )
如图,D、E分别是AB、AC上的点,DC、BE交于F,则下列结论一定正确的是( )| A. | ∠ADC>∠AEB | B. | ∠ABC>∠DFE | C. | ∠ADC>∠B | D. | ∠ADC>∠C |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图,在平行四边形ABCD中,∠ABC=60°,AB=20cm,AD=30cm,动点Q从点A出发,沿AB向点B匀速运动,速度为2cm/s,同时,动点P从点B出发,沿BC向点C匀速运动,速度为3cm/s,当点P停止运动时,点Q也随之停止运动,连接PQ,设运动的时间为t秒(0<t<10).
已知,如图,在平行四边形ABCD中,∠ABC=60°,AB=20cm,AD=30cm,动点Q从点A出发,沿AB向点B匀速运动,速度为2cm/s,同时,动点P从点B出发,沿BC向点C匀速运动,速度为3cm/s,当点P停止运动时,点Q也随之停止运动,连接PQ,设运动的时间为t秒(0<t<10).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠C=90°,P是BC边上不同于B,C的一动点,过点P作PQ⊥AB,垂足为Q,连接AP.若AC=3,BC=4,则△AQP的面积的最大值是( )
如图,在Rt△ABC中,∠C=90°,P是BC边上不同于B,C的一动点,过点P作PQ⊥AB,垂足为Q,连接AP.若AC=3,BC=4,则△AQP的面积的最大值是( )| A. | $\frac{25}{4}$ | B. | $\frac{25}{8}$ | C. | $\frac{75}{32}$ | D. | $\frac{75}{16}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | $\sqrt{3}-2$ | C. | $\sqrt{3}+2$ | D. | -$\sqrt{3}-2$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com