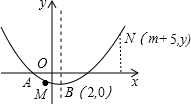
解:(1)∵4a+2b+c=0,
∴a,b,c至少有一个为正,
∵a>b>c,
∴a>0,
①当a>0,c>0时候,则b>0,所以4a+2b+c>0,与4a+2b+c=0矛盾,不合题意;
②当a>0,c<0时候,所以4a+2b+c可能等于0,
∴a>0,c<0;
故答案为:=,>,<.
(2)由题意可知:x
1x
2=2x
2=

,解得:另一根x
2=

;
(3)答:当x=m+5时,代数式ax
2+bx+c的值是正数.
理由如下:
设抛物线y=ax
2+bx+c(a≠0),则由题意可知,它经过A
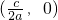
,B(2,0)点.
∵a>0,c<0,∴抛物线y=ax
2+bx+c开口向上,且

<0<2,即点A在点B左侧.
设点M的坐标为M(m,am
2+bm+c),点N的坐标为N(m+5,y).
∵代数式am
2+bm+c的值小于0,∴点M在抛物线y=ax
2+bx+c上,且点M的纵坐标为负数.
∴点M在x轴下方的抛物线上.(如图)∴x
A<x
M<x
B,即

.
∴
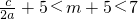
,即
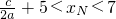
.
以下判断
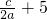
与x
B的大小关系:
∵4a+2b+c=0,a>b,a>0,
∴

.
∴
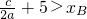
.∴
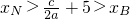
.
∵B,N两点都在抛物线的对称轴的右侧,y随x的增大而增大,
∴y
N>y
B,即y>0.
∴当x=m+5时,代数式ax
2+bx+c的值是正数.
分析:(1)根据图象可知抛物线开口向上,所以得到a大于0,又抛物线与y轴的交点在y轴的负半轴得到c小于0,由方程ax
2+bx+c=0有一根为2,得到抛物线与x轴的一个交点为(2,0),代入抛物线的解析式即可得到4a+2b+c=0;
(2)根据根与系数的关系得到两根之积为

,而一根为2,即可求出另一根;
(3)根据第(2)表示出点A的坐标,又根据(1)中判断出的a与c的正负,根据二次函数的图象可判断出A在B的左侧,设出M点的坐标为(m,am
2+bm+c),则点N的坐标为(m+5,y),根据二次函数图象可知点M在x轴的下方的抛物线上,即可得到点A,点B以及点M横坐标的大小,把关于m的不等式两边都加上5,即可得到N的横坐标的范围,然后利用做差法判断出点N与点B横坐标的大小,得到两点都在对称轴的右边,根据对称轴右边抛物线的图象为增函数,且x=2时的函数值为0,得到y大于0,即当x=m+5时,代数式ax
2+bx+c的值为正数.
点评:此题考查学生灵活运用阅读材料中给出的根与系数的关系,考查了数形结合的数学思想,要求学生掌握二次函数的图象与性质并会根据二次函数的图象判断得出a、b及c的符号,是一道多知识的综合题.

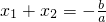 ,
,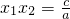 .
. 解:(1)∵4a+2b+c=0,
解:(1)∵4a+2b+c=0, ,解得:另一根x2=
,解得:另一根x2= ;
;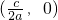 ,B(2,0)点.
,B(2,0)点. <0<2,即点A在点B左侧.
<0<2,即点A在点B左侧. .
.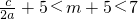 ,即
,即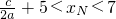 .
.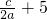 与xB的大小关系:
与xB的大小关系: .
.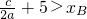 .∴
.∴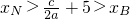 .
. ,而一根为2,即可求出另一根;
,而一根为2,即可求出另一根;

 阅读快车系列答案
阅读快车系列答案