练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．若$\sqrt{13}$的整数部分是a，则a的值等于3．

    分析 根据平方根的意义确定$\sqrt{13}$的范围，则整数部分即可求得．

    解答 解：∵$\sqrt{9}$＜$\sqrt{13}$＜$\sqrt{16}$，
    ∴3＜$\sqrt{13}$＜4，
    ∴$\sqrt{13}$的整数部分是3．
    ∴a=3，
    故答案是：3．

    点评 本题主要考查了无理数的估算，解题关键是确定无理数的整数部分即可解决问题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    20．把一根24cm长的铁丝分成两段，将每一段围成一个正方形，若这两个正方形的面积之差是12cm2，则所分成的两段铁丝中较长的是16cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．某艺术类学校进行绘画特长生的招生工作，每名考生需要参加“素描”“色彩”“速写”三个项目的测试，三个项目的满分均为100分，“素描”“色彩”“速写”按照4：4：2的比例计算得到选手最终成就，现有20名考生报名参加测试，测试结束后，考生的素描成绩如下（单位：分）：
    88，85，90，99，86，68，94，98，78，97
    96，93，89，94，89，85，80，95，89，77
    请根据上述数据，解决下列问题：
    （1）补全下面考生素描成绩的表格（每组数据含最小值不含最大值）和频数分布直方图；
    分组人数（频数）
    60-701
    70-802 
    80-909
    90-1008 
    合计20
    （2）如表为甲、乙两名选手比赛成绩的记录表，现要在甲、乙二人中录取一名，请通过计算得出谁最终被录取．
               项目
              成绩    		素描色彩速写
    甲989395
    乙9595100

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

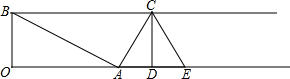    18．如图，射线BC∥射线OA，BO⊥OA，且OB=2，OA=4，过点A作AC⊥AB交射线BC于C，过点C作CD⊥射线OA交射线OA于D，A，E关于直线CD对称，将△CDE沿射线BC向左向右平移得到△C′D′E′．再将以A，B，C′，E′为顶点的四边形沿着C′D′剪开得到的两个图形拼成不重叠无缝隙的图形恰好是三角形，请写出所有符合上述条件的BC′的长6或1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．根据某研究中心公布的近几年中国互联网络发展状况统计报告的部分相关数据，绘制的统计图表如下：

    根据以上信息解答下列问题：（精确到0.01）
    （1）直接写出扇形统计图中m的值；
    （2）求从2009年到2015年，中国网民人数平均每年增长的人数是多少亿；
    （3）据2015年吉安市人口统计数据显示常住人口为481万人，其中网民数约为200万人．若2015年吉安市的网民学历结构与2015年的中国网民学历结构基本相同，请你估算2015年末该市网民学历是高中、中考、技校的约有多少万人．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图，已知△ABC中，∠ACB=90°，∠ABC=30°，AC=2，点P是边AB上的一个动点，以点P为圆心，PB的长为半径画弧，交射线BC于点D，射线PD交射线AC于点E．
    （1）当点D与点C重合时，求PB的长；
    （2）当点E在AC的延长线上时，设PB=x，CE=y，求y关于x的函数关系式，并写出定义域；
    （3）当△PAD是直角三角形时，求PB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．2016年2月6日，台湾地震，牵动着全国人民的心，地震后石家庄某中学举行了爱心捐款活动，如图时该校九年级某班学生为台湾灾区捐款情况绘制的不完整的条形统计图和扇形统计图．
    （1）求该班人数；
    （2）补全条形统计图；
    （3）求在扇形统计图中，捐款“15元人数”所在扇形的圆心角∠AOB的度数；
    （4）若该校九年级有800人，据此样本，请你估计该校九年级学生共捐款多少元？

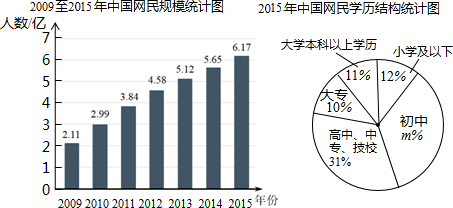
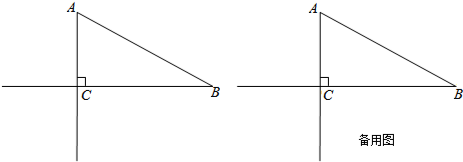
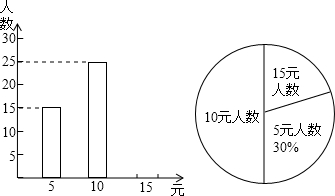
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．近似数1.30是由数x四舍五入得到的数，则数x的取值范围是（　　）
    A．1.25≤x＜1.35B．1.295≤x＜1.305C．1.25＜x＜1.35D．1.295＜x＜1.305

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．已知菱形ABCD的边长为1．∠ADC=60°，等边△AEF两边分别交边DC，CB于点E，F．
    （1）特殊发现：如图1，若点E、F分别是边DC、CB的中点．求证：菱形ABCD对角线AC、BD交点O即为等边△AEF的外心；
    （2）若点E、F始终分别在边DC、CB上移动．记等边△AEF的外心为点P．
    ①猜想验证：如图2，猜想△AEF的外心P落在哪一直线上，并加以证明；
    ②拓展运用：如图3，当△AEF面积最小时，过点P任作一直线分别交边DA于点M，交边DC的延长线于点N，试判断$\frac{1}{DM}+\frac{1}{DN}$是否为定值？若是，请求出该定值；若不是，请说明理由．

    查看答案和解析>>

    同步练习册答案