
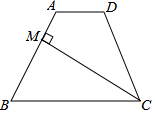
 如图,四边形ABCD中,AD∥BC,CM是∠BCD的平分线,且CM⊥AB,M为垂足,AM=$\frac{1}{3}$AB.若四边形ABCD的面积为$\frac{15}{7}$,则四边形AMCD的面积是1.
如图,四边形ABCD中,AD∥BC,CM是∠BCD的平分线,且CM⊥AB,M为垂足,AM=$\frac{1}{3}$AB.若四边形ABCD的面积为$\frac{15}{7}$,则四边形AMCD的面积是1. 分析 延长BA、CD,交点为E.依据题意可知MB=ME.然后证明△EAD∽△EBC.依据相似三角形的性质可求得△EAD和△EBC的面积,最后依据S四边形AMCD=$\frac{1}{2}$S△EBC-S△EAD求解即可.
解答 解:如图所示:延长BA、CD,交点为E.
∵CM平分∠BCD,CM⊥AB,
∴MB=ME.
又∵AM=$\frac{1}{3}$AB,
∴AE=$\frac{1}{3}$AB.
∴AE=$\frac{1}{4}$BE.
∵AD∥BC,
∴△EAD∽△EBC.
∴$\frac{{S}_{△EAD}}{{S}_{△EBC}}$=$\frac{1}{16}$.
∴S四边形ADBC=$\frac{15}{16}$S△EBC=$\frac{15}{7}$.
∴S△EBC=$\frac{16}{7}$.
∴S△EAD=$\frac{16}{7}$×$\frac{1}{16}$=$\frac{1}{7}$.
∴S四边形AMCD=$\frac{1}{2}$S△EBC-S△EAD=$\frac{8}{7}$-$\frac{1}{7}$=1.
故答案为:1.
点评 本题主要考查的是相似三角形的性质和判定,掌握本题的辅助线的作法是解题的关键.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 2.076×108 | B. | 2076×106 | C. | 0.2076×108 | D. | 2.076×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 位于张家界核心景区的贺龙铜像,是我国近百年来最大的铜像.铜像由像体AD和底座CD两部分组成.如图,在Rt△ABC中,∠ABC=70.5°,在Rt△DBC中,∠DBC=45°,且CD=2.3米,求像体AD的高度(最后结果精确到0.1米,参考数据:sin70.5°≈0.943,cos70.5°≈0.334,tan70.5°≈2.824)
位于张家界核心景区的贺龙铜像,是我国近百年来最大的铜像.铜像由像体AD和底座CD两部分组成.如图,在Rt△ABC中,∠ABC=70.5°,在Rt△DBC中,∠DBC=45°,且CD=2.3米,求像体AD的高度(最后结果精确到0.1米,参考数据:sin70.5°≈0.943,cos70.5°≈0.334,tan70.5°≈2.824)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
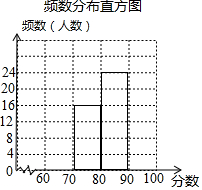 九 (1)班48名学生参加学校举行的“珍惜生命,远离毒品”只是竞赛初赛,赛后,班长对成绩进行分析,制作如下的频数分布表和频数分布直方图(未完成).余下8名学生成绩尚未统计,这8名学生成绩如下:60,90,63,99,67,99,99,68.
九 (1)班48名学生参加学校举行的“珍惜生命,远离毒品”只是竞赛初赛,赛后,班长对成绩进行分析,制作如下的频数分布表和频数分布直方图(未完成).余下8名学生成绩尚未统计,这8名学生成绩如下:60,90,63,99,67,99,99,68.| 分数段 | 频数(人数) |
| 60≤x<70 | a |
| 70≤x<80 | 16 |
| 80≤x<90 | 24 |
| 90≤x<100 | b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
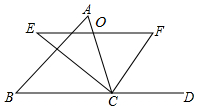 如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E、F.
如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E、F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
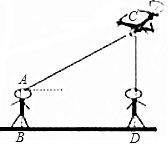 我区中小学生广播操比赛中,无人机对此次比赛的全过程进行了航拍,如图,某一时刻,无人机刚好飞至小琪头顶上方,而站在离小琪35米远的小珺仰望无人机,仰角为36°,已知小珺的眼睛离地面的距离AB为1.63m,那么此时无人机离地面大约有多高?(结果精确到0.1m)(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)
我区中小学生广播操比赛中,无人机对此次比赛的全过程进行了航拍,如图,某一时刻,无人机刚好飞至小琪头顶上方,而站在离小琪35米远的小珺仰望无人机,仰角为36°,已知小珺的眼睛离地面的距离AB为1.63m,那么此时无人机离地面大约有多高?(结果精确到0.1m)(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
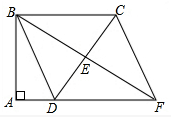 如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com