练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．小明同学在社团活动中给发明的机器人设置程序：（a，n）．机器人执行步骤是：向正前方走am后向左转n°，再依次执行相同程序，直至回到原点．现输入a=4，n=60，那么机器人回到原点共走了24m．

    分析 根据多边形的外角和定理解可求出机器人共走了多少米．

    解答 解：由题意可知：n=60°，
    由于多边形的外角和为360°，
    ∴该多边形的边数为：$\frac{360}{60}$=6
    ∴机器人所走的路径是正六边形，
    ∴机器人回到原点共走了4×6=24m
    故答案为：24m

    点评 本题考查多边形的外角和，解题的关键是熟练运用多边形外角和性质，本题属于基础题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    6．将下列长度的三根木棒首尾顺次连接，不能组成直角三角形的是（　　）
    A．1，$\sqrt{2}$，$\sqrt{3}$B．5，12，13C．6，8，10D．$\sqrt{3}$，$\sqrt{4}$，$\sqrt{5}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．已知a：b=3：5，a：c=6：7，则a：b：c=6：10：7．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．二元一次方程5x+2y=15的正整数解是$\left\{\begin{array}{l}{x=1}\\{y=5}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．如图，PA，PB切⊙O于两点，若∠APB=60°，⊙O的半径为6，则阴影部分的面积为36$\sqrt{3}$-12π．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．正方形ABCD中，E为DC边上一点，且DE=1，将AE绕点E顺时针旋转90°得到EF，连接AF，FC，则FC=$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

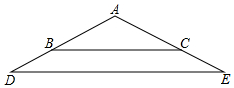    13．在等腰三角形ABC和等腰三角形ADE中，∠BAC=∠DAE=120°，AB=2，AD=3，点A、B、D在同一条直线上，将△ADE绕点A旋转180°，在旋转过程中，直线BD、CE的交点为点F，直接写出点F经过的路径的长度4π．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．如图，在?ABCD中，AC⊥CD，E是AD的中点，若CE=4，则BC的长是8．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．如图，在直角坐标系中，直线l是经过点（0，1）且平行于x轴的直线，则点（2，-2）关于直线l的对称点的坐标为（2，4）．

    查看答案和解析>>

    同步练习册答案