
【题目】在平而直角坐标系中,已知点![]() ,直线
,直线![]() 经过点
经过点![]() .抛物线
.抛物线![]() 恰好经过
恰好经过![]() 三点中的两点.
三点中的两点.
![]() 判断点
判断点![]() 是否在直线
是否在直线![]() 上.并说明理由;
上.并说明理由;
![]() 求
求![]() 的值;
的值;
![]() 平移抛物线
平移抛物线![]() ,使其顶点仍在直线
,使其顶点仍在直线![]() 上,求平移后所得抛物线与
上,求平移后所得抛物线与![]() 轴交点纵坐标的最大值.
轴交点纵坐标的最大值.
【答案】(1)点![]() 在直线
在直线![]() 上,理由见详解;(2)a=-1,b=2;(3)
上,理由见详解;(2)a=-1,b=2;(3)![]()
【解析】
(1)先将A代入![]() ,求出直线解析式,然后将将B代入看式子能否成立即可;
,求出直线解析式,然后将将B代入看式子能否成立即可;
(2)先跟抛物线![]() 与直线AB都经过(0,1)点,且B,C两点的横坐标相同,判断出抛物线只能经过A,C两点,然后将A,C两点坐标代入
与直线AB都经过(0,1)点,且B,C两点的横坐标相同,判断出抛物线只能经过A,C两点,然后将A,C两点坐标代入![]() 得出关于a,b的二元一次方程组;
得出关于a,b的二元一次方程组;
(3)设平移后所得抛物线的对应表达式为y=-(x-h)2+k,根据顶点在直线![]() 上,得出k=h+1,令x=0,得到平移后抛物线与y轴交点的纵坐标为-h2+h+1,在将式子配方即可求出最大值.
上,得出k=h+1,令x=0,得到平移后抛物线与y轴交点的纵坐标为-h2+h+1,在将式子配方即可求出最大值.
(1)点![]() 在直线
在直线![]() 上,理由如下:
上,理由如下:
将A(1,2)代入![]() 得
得![]() ,
,
解得m=1,
∴直线解析式为![]() ,
,
将B(2,3)代入![]() ,式子成立,
,式子成立,
∴点![]() 在直线
在直线![]() 上;
上;
(2)∵抛物线![]() 与直线AB都经过(0,1)点,且B,C两点的横坐标相同,
与直线AB都经过(0,1)点,且B,C两点的横坐标相同,
∴抛物线只能经过A,C两点,
将A,C两点坐标代入![]() 得
得![]() ,
,
解得:a=-1,b=2;
(3)设平移后所得抛物线的对应表达式为y=-(x-h)2+k,
∵顶点在直线![]() 上,
上,
∴k=h+1,
令x=0,得到平移后抛物线与y轴交点的纵坐标为-h2+h+1,
∵-h2+h+1=-(h-![]() )2+
)2+![]() ,
,
∴当h=![]() 时,此抛物线与
时,此抛物线与![]() 轴交点的纵坐标取得最大值
轴交点的纵坐标取得最大值![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:如图,二次函数的图象与x轴交于A(-2,0),B(4,0)两点,且函数的最大值为9.
(1)求二次函数的解析式;
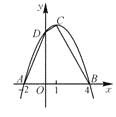
(2)设此二次函数图象的顶点为C,与y轴交点为D,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“新冠”疫情期间,全国人民“众志成城,同心抗疫”,某商家决定将一个月获得的利润全部捐赠给社区用于抗疫.已知商家购进一批产品,成本为10元/件,拟采取线上和线下两种方式进行销售.调查发现,线下的月销量![]() (单位:件)与线下售价
(单位:件)与线下售价![]() (单位:元/件,
(单位:元/件,![]() )满足一次函数的关系,部分数据如下表:
)满足一次函数的关系,部分数据如下表:

(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若线上售价始终比线下每件便宜2元,且线上的月销量固定为400件.试问:当![]() 为多少时,线上和线下月利润总和达到最大?并求出此时的最大利润.
为多少时,线上和线下月利润总和达到最大?并求出此时的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点E、F、G、H分别是边AB、BC、CD和DA的中点,连接EF、FG、GH和HE.若EH=2EF,则下列结论正确的是
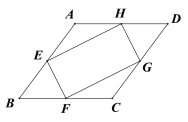
A. AB=![]() EF B. AB=2EF C. AB=
EF B. AB=2EF C. AB=![]() EF D. AB=
EF D. AB=![]() EF
EF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于已知的两个函数,任取自变量![]() 的一个值,当
的一个值,当![]() 时,它们对应的函数值相等;当
时,它们对应的函数值相等;当![]() 时,它们对应的函数值互为相反数,我们称这样的两个函数互为相关函数.例如:正比例函数
时,它们对应的函数值互为相反数,我们称这样的两个函数互为相关函数.例如:正比例函数![]() ,它的相关函数为
,它的相关函数为![]() .
.
(1)已知点![]() 在一次函数
在一次函数![]() 的相关函数的图像上,求
的相关函数的图像上,求![]() 的值;
的值;
(2)已知二次函数![]() .
.
①当点![]() 在这个函数的相关函数的图像上时,求
在这个函数的相关函数的图像上时,求![]() 的值;
的值;
②当![]() 时,求函数
时,求函数![]() 的相关函数的最大值和最小值.
的相关函数的最大值和最小值.
(3)在平面直角坐标系中,点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,连结
,连结![]() .直接写出线段
.直接写出线段![]() 与二次函数
与二次函数![]() 的相关函数的图像有两个公共点时
的相关函数的图像有两个公共点时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年植树节期间,某景观园林公司购进一批成捆的![]() ,
,![]() 两种树苗,每捆
两种树苗,每捆![]() 种树苗比每捆
种树苗比每捆![]() 种树苗多10棵,每捆
种树苗多10棵,每捆![]() 种树苗和每捆
种树苗和每捆![]() 种树苗的价格分别是630元和600元,而每棵
种树苗的价格分别是630元和600元,而每棵![]() 种树苗和每棵
种树苗和每棵![]() 种树苗的价格分别是这一批树苗平均每棵价格的0.9倍和1.2倍.
种树苗的价格分别是这一批树苗平均每棵价格的0.9倍和1.2倍.
(1)求这一批树苗平均每棵的价格是多少元?
(2)如果购进的这批树苗共5500棵,![]() 种树苗至多购进3500棵,为了使购进的这批树苗的费用最低,应购进
种树苗至多购进3500棵,为了使购进的这批树苗的费用最低,应购进![]() 种树苗和
种树苗和![]() 种树苗各多少棵?并求出最低费用.
种树苗各多少棵?并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
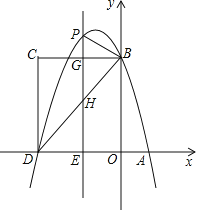
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
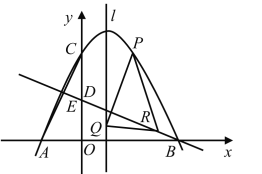
【题目】如图,已知抛物线![]() 经过
经过![]() ,
,![]() ,
,![]() 三点.
三点.
(1)求该抛物线的解析式;
(2)经过点B的直线交y轴于点D,交线段![]() 于点E,若
于点E,若![]() .
.
①求直线![]() 的解析式;
的解析式;
②已知点Q在该抛物线的对称轴l上,且纵坐标为1,点P是该抛物线上位于第一象限的动点,且在l右侧.点R是直线![]() 上的动点,若
上的动点,若![]() 是以点Q为直角顶点的等腰直角三角形,求点P的坐标.
是以点Q为直角顶点的等腰直角三角形,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() 与x轴交于点A,B(点A在点B的左边),与y轴交于点C,点D是该抛物线的顶点.
与x轴交于点A,B(点A在点B的左边),与y轴交于点C,点D是该抛物线的顶点.
(1)如图1,连接CD,求线段CD的长;
(2)如图2,点P是直线AC上方抛物线上一点,PF⊥x轴于点F,PF与线段AC交于点E;将线段OB沿x轴左右平移,线段OB的对应线段是O1B1,当PE+![]() EC的值最大时,求四边形PO1B1C周长的最小值,并求出对应的点O1的坐标;
EC的值最大时,求四边形PO1B1C周长的最小值,并求出对应的点O1的坐标;
(3)如图3,点H是线段AB的中点,连接CH,将△OBC沿直线CH翻折至△O2B2C的位置,再将△O2B2C绕点B2旋转一周在旋转过程中,点O2,C的对应点分别是点O3,C1,直线O3C1分别与直线AC,x轴交于点M,N.那么,在△O2B2C的整个旋转过程中,是否存在恰当的位置,使△AMN是以MN为腰的等腰三角形?若存在,请直接写出所有符合条件的线段O2M的长;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com