
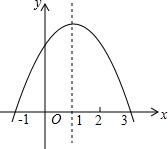
 已知二次函数y=ax2+bx+c(a、b、c是常数),图象如图所示,则当x满足的条件是-1<x<3时,y>0.
已知二次函数y=ax2+bx+c(a、b、c是常数),图象如图所示,则当x满足的条件是-1<x<3时,y>0.  冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
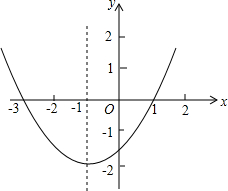 抛物线y=$\frac{1}{2}$(x+1)2-2.
抛物线y=$\frac{1}{2}$(x+1)2-2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
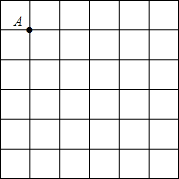 作图题:如图,在6×6的正方形网格中,每个小正方形的边长都为1,请在所给网格中按下列要求画出图形.
作图题:如图,在6×6的正方形网格中,每个小正方形的边长都为1,请在所给网格中按下列要求画出图形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
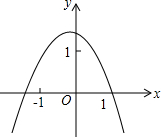 从如图所示的二次函数y=ax2+bx+c的图象中,孔明同学观察得出了下面四条信息:①b2-4ac>0;②c>1;(3)2a-b<0;(4)a+b+c<0.你认为其中错误的有( )
从如图所示的二次函数y=ax2+bx+c的图象中,孔明同学观察得出了下面四条信息:①b2-4ac>0;②c>1;(3)2a-b<0;(4)a+b+c<0.你认为其中错误的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com