
【题目】在如图的正方形网格中,每一个小正方形的边长为1.格点三角形ABC(顶点是网格线交点的三角形)的顶点A、C的坐标分别是(﹣4,6),(﹣1,4).

(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出△ABC关于x轴对称的△A1B1C1;
(3)△ABC 直角三角形(填“是”或“不是”);
(4)请在y轴上画一点P,使△PB1C的周长最小,并写出点P的坐标.
【答案】(1)平面直角坐标系见详解,(2)见详解,(3)不是,(4)P点见详解作图,![]() .
.
【解析】
(1)根据A点坐标建立平面直角坐标系即可,
(2)分别作出各点关于x轴的对称点,再顺次连接即可,
(3)利用勾股定理分别求出AB,BC,AC的长,即可证明是否满足勾股定理,
(4) 作出点B关于y轴的对称点B2,连接B2交y轴于点P,则P点即为所求.
解:(1)平面直角坐标系如图.
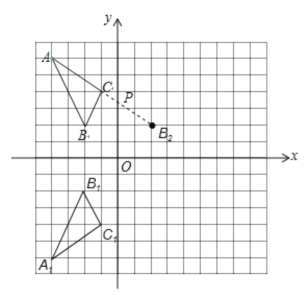
(2)△ABC关于x轴对称的△A1B1C1如上图.
(3)A、C的坐标分别是(﹣4,6),(﹣1,4),且每一个小正方形的边长为1,利用勾股定理求得有![]()
有![]() 即
即![]()
故△ABC不是直角三角形.
(4))作点B关于y轴的对称点![]() ,连接A
,连接A![]() 交y轴于点P,则点P即为所求.
交y轴于点P,则点P即为所求.
设直线A![]() 的解析式为y=kx+b(k≠0),
的解析式为y=kx+b(k≠0),
∵A(-4,6),![]() (2,2),
(2,2),
∴![]() 解得
解得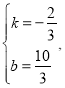
∴直线A![]() 的解析式为:
的解析式为:![]()
∴当x=0时,y=![]() ,
,
∴P点的坐标为 ![]() .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,把n个边长为1的正方形拼接成一排,求得tan∠BA1C=1,tan∠BA2C=![]() ,tan∠BA3C=
,tan∠BA3C=![]() ,计算tan∠BA4C=_____,…按此规律,写出tan∠BAnC=_____(用含n的代数式表示).
,计算tan∠BA4C=_____,…按此规律,写出tan∠BAnC=_____(用含n的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若A的对应点A2的坐标为(0,4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般地,“任意三角形都是自相似图形”,只要顺次连接三角形各边中点,则可将原三角形分割为四个都与它自己相似的小三角形.我们把![]() (图乙)第一次顺次连接各边中点所进行的分割,称为
(图乙)第一次顺次连接各边中点所进行的分割,称为![]() 阶分割(如图
阶分割(如图![]() );把
);把![]() 阶分割得出的
阶分割得出的![]() 个三角形再分别顺次连接它的各边中点所进行的分割,称为
个三角形再分别顺次连接它的各边中点所进行的分割,称为![]() 阶分割(如图
阶分割(如图![]() )…,依此规则操作下去.
)…,依此规则操作下去.![]() 阶分割后得到的每一个小三角形都是全等三角形(
阶分割后得到的每一个小三角形都是全等三角形(![]() 为正整数),设此时小三角形的面积为
为正整数),设此时小三角形的面积为![]() .请写出一个反映
.请写出一个反映![]() ,
,![]() ,
,![]() 之间关系的等式________.
之间关系的等式________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把长与宽之比为![]() 的矩形纸片称为标准纸.不难发现,将一张标准纸如图一次又一次对开后,所得的矩形纸片都是标准纸.现有一张标准纸
的矩形纸片称为标准纸.不难发现,将一张标准纸如图一次又一次对开后,所得的矩形纸片都是标准纸.现有一张标准纸![]() ,
,![]() ,
,![]() ,那么把它第
,那么把它第![]() 次对开后所得标准纸的周长是________.
次对开后所得标准纸的周长是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为![]() 个单位长度的小正方形组成的网格中,给出了格点
个单位长度的小正方形组成的网格中,给出了格点![]() 和
和![]() (顶点是网格线的交点).点
(顶点是网格线的交点).点![]() 、
、![]() 坐标为
坐标为![]() ,
,![]() .
.
![]() 观察图形填空:
观察图形填空:![]() 是由
是由![]() 绕________点顺时针旋转________度得到的;
绕________点顺时针旋转________度得到的;
![]() 把
把![]() 中的图形作为一个新的”基本图形“,将新的基本图形绕
中的图形作为一个新的”基本图形“,将新的基本图形绕![]() 点顺时针旋转
点顺时针旋转![]() 度,请作出旋转后的图形,其中,
度,请作出旋转后的图形,其中,![]() 、
、![]() 、
、![]() 、
、![]() 的对应点分别为
的对应点分别为![]() 、
、![]() 、
、![]() 、
、![]() .依次连接
.依次连接![]() 、
、![]() 、
、![]() 、
、![]() ,则四边形
,则四边形![]() 的形状为________;
的形状为________;
![]() 以
以![]() 点为位似中心,位似比为
点为位似中心,位似比为![]() (原图与新图对应边的比为
(原图与新图对应边的比为![]() ),作出四边形
),作出四边形![]() 的位似图形.
的位似图形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于(2,0)、(1,0),与y轴交于C,直线l1经过点C且平行于x轴,与抛物线的另一个交点为D,将直线l1向下平移t个单位得到直线l2,l2与抛物线交于A、B两点.
x2+bx+c与x轴交于(2,0)、(1,0),与y轴交于C,直线l1经过点C且平行于x轴,与抛物线的另一个交点为D,将直线l1向下平移t个单位得到直线l2,l2与抛物线交于A、B两点.


(1)求抛物线解析式及点C的坐标;
(2)当t=2时,探究△ABC的形状,并说明理由;
(3)在(2)的条件下,点M(m,0)在x轴上自由运动,过M作MN⊥x轴,交直线BC于P,交抛物线于N,若三个点M、N、P中恰有一个点是其他两个点连线段的中点(三点重合除外),则称M、N、P三点为“共谐点”,请直接写出使得M、P、N三点为“共谐点”的m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,C是AB上一点,点D,E分别在AB两侧,AD∥BE,且AD=BC,BE=AC.

(1)求证:CD=CE;
(2)连接DE,交AB于点F,猜想△BEF的形状,并给予证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com