
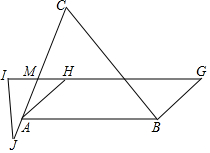
 如图所示,已知H为△ABC的垂心,点G满足四边形ABGH为平行四边形.I为直线GH上的点,AC交GI于M.且IM=MH.J为CA延长线上一点,且IJ=AH,求证:I、J、G、C四点共圆.(坐标法不得分)
如图所示,已知H为△ABC的垂心,点G满足四边形ABGH为平行四边形.I为直线GH上的点,AC交GI于M.且IM=MH.J为CA延长线上一点,且IJ=AH,求证:I、J、G、C四点共圆.(坐标法不得分) 分析 延长CH,BH分别交AB,AC于D,E,由H为△ABC的垂心,得到CD⊥AB,BE⊥AC,过I作IK⊥AC于K,于是得到∠IKM=∠EMH=90°,在根据全等三角形的性质得到HE=IK,根据相似三角形的性质得到$\frac{CH}{AB}=\frac{EH}{AE}$,根据平行四边形的性质得到HG=AB,推出△CHG∽△HEA,于是得到∠GCH=∠EHA,等量代换得到∠GCH=∠JIK,求得∠JIG=∠JCG,于是得到结论.
解答 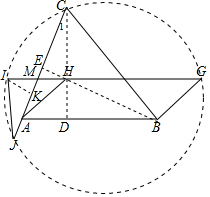 证明:延长CH,BH分别交AB,AC于D,E,
证明:延长CH,BH分别交AB,AC于D,E,
∵H为△ABC的垂心,
∴CD⊥AB,BE⊥AC,
过I作IK⊥AC于K,
∴∠IKM=∠EMH=90°,
在△IKM与HEM中,$\left\{\begin{array}{l}{∠HEM=∠IKM=90°}\\{∠IMK=∠EMH}\\{IM=HM}\end{array}\right.$,
∴△MKI≌△MEH,
∴HE=IK,
在Rt△EHA与△RtKIJ中,$\left\{\begin{array}{l}{HE=IK}\\{AH=IJ}\end{array}\right.$,
∴Rt△EHA≌△RtKIJ,
∴∠EHA=∠KIJ,
∵∠AEB=∠CEH=90°,∠ACH=∠ABE,
∴△CHE∽△BAE,
∴$\frac{CH}{AB}=\frac{EH}{AE}$,
∵四边形ABGH为平行四边形,
∴HG=AB,
∴$\frac{CH}{HG}$=$\frac{EH}{AE}$,
∵∠AEH=∠CHG=90°,
∴△CHG∽△HEA,
∴∠GCH=∠EHA,
∴∠GCH=∠JIK,
∴∠JCG=∠KIJ+∠MIK,
∠JCG=∠GCH+∠JCH,
∴∠JIG=∠JCG,
∴I、J、G、C四点共圆.
点评 本题考查了四点共圆,全等三角形的判定与性质,相似三角形的判定和性质,三角形的垂心的性质,平行四边形的判定和性质,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:选择题
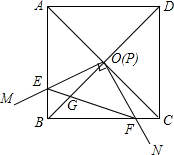 如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,∠MPN为直角,使点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM,PN分别交AB,BC于E,F两点,连接EF交OB于点G,则下列结论:①EF=$\sqrt{2}$OE;②S四边形OEBF:S正方形ABCD=1:4;③BE+BF=$\sqrt{2}$OA;④在旋转过程中,当△BEF与△COF的面积之和最大时,AE=$\frac{3}{4}$;⑤OG•BD=AE2+CF2.其中结论正确的个数是( )
如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,∠MPN为直角,使点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM,PN分别交AB,BC于E,F两点,连接EF交OB于点G,则下列结论:①EF=$\sqrt{2}$OE;②S四边形OEBF:S正方形ABCD=1:4;③BE+BF=$\sqrt{2}$OA;④在旋转过程中,当△BEF与△COF的面积之和最大时,AE=$\frac{3}{4}$;⑤OG•BD=AE2+CF2.其中结论正确的个数是( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{x+1}{x-y}$=$\frac{-x+1}{x-y}$ | B. | $\frac{{x}^{2}+{y}^{2}}{x+y}$=x+y | ||
| C. | $\frac{0.5a+b}{0.2a-0.3b}$=$\frac{5a+10b}{2a-3b}$ | D. | $\frac{a-b}{a+b}$=$\frac{b-a}{b+a}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 运行区间 | 大人票价 | 学生票价 | |||
| 出发站 | 终点站 | 一等座 | 二等座 | 一等座 | 二等座 |
| 泉州 | 福州 | 65(元) | 54(元) | 65(元) | 40(元) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com