
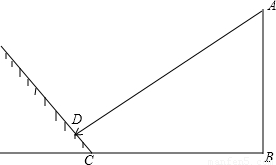
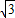 AB,从而可计算出AB.
AB,从而可计算出AB.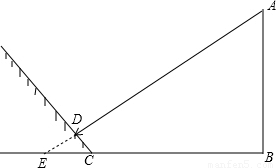
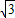 AB,
AB,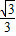 =7
=7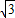 (m).
(m).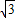 m.
m.

科目:初中数学 来源:鼎尖助学系列—同步练习(数学 八年级下册)、期末测试卷 题型:044
| |||||||||||
查看答案和解析>>
科目:初中数学 来源: 题型:044
小琳同学学习了“投影(一)”这一节以后,就想利用树影测量树高,但这棵树离大楼太近,影子不全落在地上,有一部分影子在墙上(如图所示),她在某时刻测得留在墙上的影子为1.2m,测得地面上的影子为2.7m巧的是她拿的竹竿的影长也是1.2m,竹竿的长为1.08m,她是怎样求得树高AB的,结果是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com