Question

14．在?ABCD中，AB=5，BC=10，BC边上的高AM=4，过BC边上的动点E（不与点B，C重合）作直线AB的垂线，EF与DC的延长线相交于点G．
（Ⅰ）如图①，当点E与点M重合时，求EF的长；
（Ⅱ）如图②，当点E为BC的中点时，连结DE，DF，求△DEF的面积；
（Ⅲ）当点E在BC上运动时，△BEF与△CEG的周长之间有何关系？请说明理由．

Answer 1

分析 （I）先由勾股定理求BM的长，再利用面积法求EF；
（II）要想求△DEF的面积，需要求底边EF和高DG的长，先证明△ABM≌△EBF，得EF=AM=4，再证明FG⊥DG，证明△BEF≌△CEG，得CG=3，求出DG=8，代入面积公式可以求△DEF的面积；
（III）过点C作CH⊥AB，垂足为H，利用勾股定理求BH的长，写出△BEF与△CEG的周长之和，发现：EF+EG=FG=8，BF+CG=BH=6，从而求出面积和为24，是定值．

解答 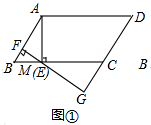解：（Ⅰ）如图①，∵AB=5，AM=4，AM⊥BC，
∴BM=$\sqrt{A{B}^{2}-A{M}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3，
∵S_△ABM=$\frac{1}{2}$AM•BM=$\frac{1}{2}$AB•EF，
∴EF=$\frac{AM•BM}{AB}$=$\frac{4×3}{5}$=$\frac{12}{5}$．        
（Ⅱ）如图②，∵E为BC中点，BC=10，
∴BE=CE=5，
∴AB=BE=5，
∵EF⊥AB，AM⊥BC，
∴∠AMB=∠EFB=90°，
∵∠B=∠B，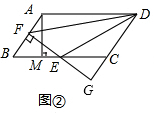
∴△ABM≌△EBF，
∴EF=AM=4，BF=BM=3，
∵四边形ABCD为平行四边形，
∴AB∥DG，
∴FG⊥DG，∠B=∠ECG，
∵∠BFE=∠G=90°，
∴△BEF≌△CEG，
∴CG=BF=3，EF=EG=4，
∴DG=CD+CG=5+3=8，
∴S_△DEF=$\frac{1}{2}$EF•DG=$\frac{1}{2}$×4×8=16；       
（Ⅲ）图③，
过点C作CH⊥AB，垂足为H，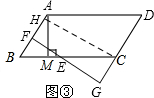
∴HC⊥DG，
∴四边形HFGC为矩形，
∴HC=FG=8，CG=FH，
∴BH=$\sqrt{B{C}^{2}-C{H}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6，
∵△BFE和△CEG的周长之和为：BE+EF+BF+EC+CG+EG，
=BC+FG+BH，
=10+8+6，
=24，
∴△BEE与△CEG的周长之和为定值24．

点评 本题是四边形的综合题，考查了平行四边形、全等三角形、矩形的性质和判定；在直角三角形中，常利用面积法求边或对应高的长，同时要注意动点E的运动路径，注意运用好标题的条件和各小题的附加条件，认真审题，尤其对于周长的变化量，要根据周长定义将三边的和表示出来，再观察其特点，总结其变化规律．