
 如图,在 Rt△ABC中,∠ACB=90°,CD⊥AB于D,tan∠B=$\frac{1}{3}$,且BC=9 cm,求AC,AB及CD的长.
如图,在 Rt△ABC中,∠ACB=90°,CD⊥AB于D,tan∠B=$\frac{1}{3}$,且BC=9 cm,求AC,AB及CD的长. 分析 根据∠B的正切求解可得AC,利用勾股定理列式计算即可得到AB,再利用△ABC的面积列方程求解即可得到CD.
解答 解:∵tan∠B=$\frac{AC}{BC}$,
∴AC=tanB•BC=$\frac{1}{3}$×9=3cm,
在Rt△ABC中,根据勾股定理得,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{9}^{2}}$=3$\sqrt{10}$cm;
∵CD⊥AB,
∴S△ABC=$\frac{1}{2}$AB•CD=$\frac{1}{2}$BC•AC,
即$\frac{1}{2}$×3$\sqrt{10}$•CD=$\frac{1}{2}$×9×3,
解得CD=$\frac{9\sqrt{10}}{10}$cm.
综上:AC=3cm,AB=3$\sqrt{10}$cm,CD=$\frac{9\sqrt{10}}{10}$cm.
点评 本题考查了解直角三角形,主要是利用锐角三角函数的概念解直角三角形,勾股定理和三角形的面积.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
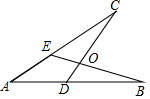 如图,点D,E分别在AB,AC上,AD=AE,BE与CD交于点O,下列条件不能判定△ABE≌△ACD的是( )
如图,点D,E分别在AB,AC上,AD=AE,BE与CD交于点O,下列条件不能判定△ABE≌△ACD的是( )| A. | ∠B=∠C | B. | BE=CD | C. | AB=AC | D. | ∠CEB=∠BDC |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}+\sqrt{3}=2\sqrt{3}$ | B. | $\sqrt{3}+\sqrt{3}=\sqrt{6}$ | C. | $\sqrt{3}×\sqrt{3}=2\sqrt{3}$ | D. | $2+\sqrt{3}=2\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
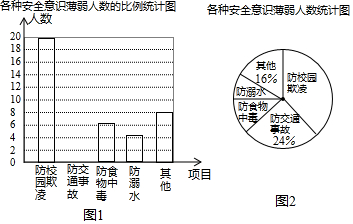
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
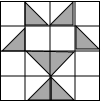 如果小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,每块方砖大小、质地完全一致,那么它最终停留在黑色区域的概率是( )
如果小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,每块方砖大小、质地完全一致,那么它最终停留在黑色区域的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
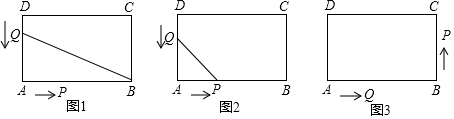
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com