
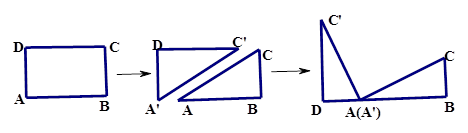
将矩形![]() 纸片沿对角线
纸片沿对角线![]() 剪开,得
剪开,得![]() 和
和![]() ,如图(1-1)所示.将
,如图(1-1)所示.将![]() 的顶点
的顶点![]() 与点
与点![]() 重合,并绕点
重合,并绕点![]() 按逆时针方向旋转,使点
按逆时针方向旋转,使点![]() 、
、![]() 、
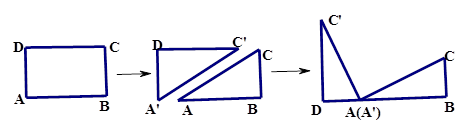
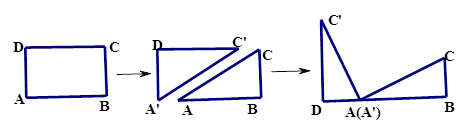
、![]() 在同一条直线上,如图(1-2)所示.
在同一条直线上,如图(1-2)所示.
1.观察图可知:与BC相等的线段是______,![]() =_______;
=_______;
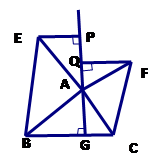
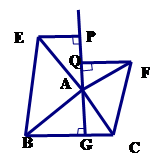
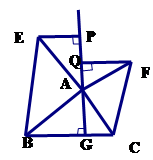
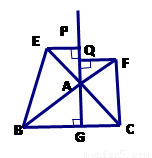
2.如图(2),![]() 中,
中,![]() 于点
于点![]() ,以
,以![]() 为直角顶点,分别以
为直角顶点,分别以![]() 、
、![]() 为直角边,向
为直角边,向![]() 外作等腰
外作等腰![]() 和等腰
和等腰![]() ,过点
,过点![]() 作射线
作射线![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() . 求证:
. 求证:![]() .
.
3.如图(3),![]() 中,
中,![]() 于点
于点![]() ,以
,以![]() 为直角顶点,分别以
为直角顶点,分别以![]() 、
、![]() 为直角边,向
为直角边,向![]() 外作
外作![]() 和
和![]() ,过点
,过点![]() 作射线
作射线![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() .若
.若![]() ,试探究
,试探究![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.

科目:初中数学 来源: 题型:
 纸片沿对角线
纸片沿对角线 剪开,得
剪开,得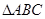 和
和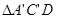 ,如图(1-1)所示.将
,如图(1-1)所示.将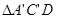 的顶点
的顶点 与点
与点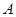 重合,并绕点
重合,并绕点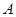 按逆时针方向旋转,使点
按逆时针方向旋转,使点 、
、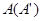 、
、 在同一条直线上,如图(1-2)所示.
在同一条直线上,如图(1-2)所示.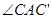 =_______;
=_______;
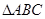 中,
中,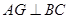 于点
于点 ,以
,以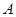 为直角顶点,分别以
为直角顶点,分别以 、
、 为直角边,向
为直角边,向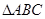 外作等腰
外作等腰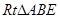 和等腰
和等腰 ,过点
,过点 作射线
作射线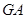 的垂线,垂足分别为
的垂线,垂足分别为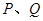 . 求证:
. 求证: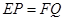 .
.
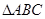 中,
中,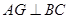 于点
于点 ,以
,以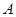 为直角顶点,分别以
为直角顶点,分别以 、
、 为直角边,向
为直角边,向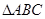 外作
外作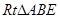 和
和 ,过点
,过点 作射线
作射线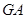 的垂线,垂足分别为
的垂线,垂足分别为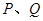 .若
.若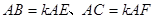 ,试探究
,试探究 与
与 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏宿迁四校八年级5月联考数学试卷(带解析) 题型:解答题
将矩形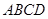 纸片沿对角线
纸片沿对角线 剪开,得
剪开,得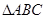 和
和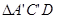 ,如图(1-1)所示.将
,如图(1-1)所示.将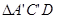 的顶点
的顶点 与点
与点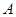 重合,并绕点
重合,并绕点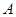 按逆时针方向旋转,使点
按逆时针方向旋转,使点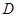 、
、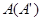 、
、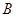 在同一条直线上,如图(1-2)所示.
在同一条直线上,如图(1-2)所示.
【小题1】观察图可知:与BC相等的线段是______,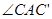 =_______;
=_______;
【小题2】如图(2),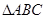 中,
中, 于点
于点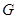 ,以
,以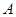 为直角顶点,分别以
为直角顶点,分别以 、
、 为直角边,向
为直角边,向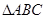 外作等腰
外作等腰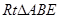 和等腰
和等腰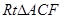 ,过点
,过点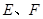 作射线
作射线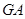 的垂线,垂足分别为
的垂线,垂足分别为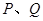 . 求证:
. 求证: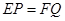 .
.
【小题3】如图(3),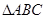 中,
中, 于点
于点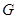 ,以
,以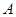 为直角顶点,分别以
为直角顶点,分别以 、
、 为直角边,向
为直角边,向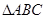 外作
外作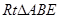 和
和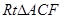 ,过点
,过点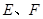 作射线
作射线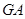 的垂线,垂足分别为
的垂线,垂足分别为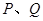 .若
.若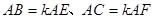 ,试探究
,试探究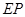 与
与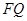 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.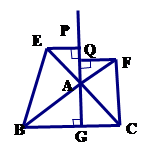
查看答案和解析>>
科目:初中数学 来源:2013届江苏宿迁四校八年级5月联考数学试卷(解析版) 题型:解答题
将矩形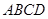 纸片沿对角线
纸片沿对角线 剪开,得
剪开,得 和
和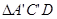 ,如图(1-1)所示.将
,如图(1-1)所示.将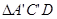 的顶点
的顶点 与点
与点 重合,并绕点
重合,并绕点 按逆时针方向旋转,使点
按逆时针方向旋转,使点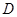 、
、 、
、 在同一条直线上,如图(1-2)所示.
在同一条直线上,如图(1-2)所示.
1.观察图可知:与BC相等的线段是______,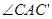 =_______;
=_______;
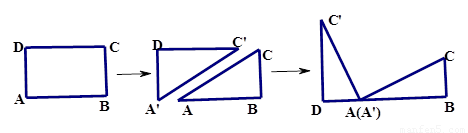
2.如图(2), 中,
中, 于点
于点 ,以
,以 为直角顶点,分别以
为直角顶点,分别以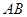 、
、 为直角边,向
为直角边,向 外作等腰
外作等腰 和等腰
和等腰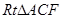 ,过点
,过点 作射线
作射线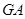 的垂线,垂足分别为
的垂线,垂足分别为 . 求证:
. 求证: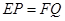 .
.

3.如图(3), 中,
中, 于点
于点 ,以
,以 为直角顶点,分别以
为直角顶点,分别以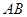 、
、 为直角边,向
为直角边,向 外作
外作 和
和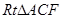 ,过点
,过点 作射线
作射线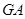 的垂线,垂足分别为
的垂线,垂足分别为 .若
.若 ,试探究
,试探究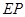 与
与 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com