Question

19．在梯形ABCD中，AD∥BC，AB⊥BC，AD=2，AB=3，BC=6，如果CE平分∠BCD交边AB于点E，那么DE的长为$\sqrt{5}$．

Answer 1

分析 方法一：要求DE的长，只要求出AE的长即可，要求AE，需要构造三角形相似，只要做出合适的辅助线即可，根据题意可以求出AE的长，本题得以解决；方法二：根据勾股定理和角平分线到角的两边的距离相等、等积法可以求得DE的长．

解答 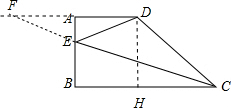解：方法一：作DH⊥BC于点H，延长CE交DA的延长线于点F，
∵AD=2，AB=3，BC=6，
∴CH=6-2=4，DH=3，
∴CD=5，
∵CE平分∠BCD交边AB于点E，AD∥BC，AB⊥BC，
∴∠DCF=∠BDF=∠DFC，
∴DF=DC=5，
∴AF=3，
∴△FAE∽△CBE，
∴$\frac{AF}{BC}=\frac{AE}{BE}$，
即$\frac{3}{6}=\frac{AE}{BE}$，
∵AE+BE=3，
解得，AE=1，
∴DE=$\sqrt{A{E}^{2}+A{D}^{2}}=\sqrt{{1}^{2}+{2}^{2}}=\sqrt{5}$，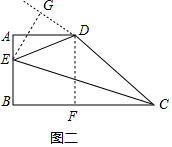
故答案为：$\sqrt{5}$．
方法二：作DF⊥BC于点F，作EG⊥CD交CD的延长线于点G，如右图所示，
由已知可得，AD=BF=2，AB=DF=3，
∴CD=5，
∵CE平分∠BCD交边AB于点E，
∴EG=EB，
设AE=a，则EB=3-a，
∴EG=3-a，
∴$\frac{（AD+BC）•AB}{2}=\frac{AD•AE}{2}+$$\frac{BC•EB}{2}+\frac{CD•EG}{2}$，
即$\frac{（2+6）×3}{2}=\frac{2a}{2}+\frac{6（3-a）}{2}+\frac{5（3-a）}{2}$，
解得，a=1，
即AE=1，
∴DE=$\sqrt{A{E}^{2}+A{D}^{2}}=\sqrt{{1}^{2}+{2}^{2}}=\sqrt{5}$，
故答案为：$\sqrt{5}$．

点评 本题考查梯形，解题的关键是明确题意，做出合适的辅助线，利用三角形的相似和数形结合的思想解答．