
【题目】如图,在直角坐标系中,点A(2,0),点B (0,1),过点A的直线l垂直于线段AB,点P是直线l上一动点,过点P作PC⊥x轴,垂足为C,把△ACP沿AP翻折![]() ,使点C落在点D处,若以A,D,P为顶点的三角形与△ABP相似,则所有满足此条件的点P的坐标为___________________________.
,使点C落在点D处,若以A,D,P为顶点的三角形与△ABP相似,则所有满足此条件的点P的坐标为___________________________.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】斜拉索桥是利用一组组钢索,把桥面重力传递到耸立在两侧的高塔上的桥梁,它不用建造桥墩,为了保持受力平衡,每相对的两根斜拉索长度必须一样,如图所示。AB表示最长的一根斜拉索已经被固定在桥面上,在施工时如何找出相对的斜拉索在桥面的位置?说明你的理由。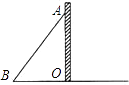
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司推出①、②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系如图所示.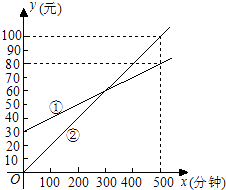
(1)有月租费的收费方式是(填①或②),月租费是元;
(2)分别求出①、②两种收费方式中y与自变量x之间的函数关系式;
(3)请你根据用户通讯时间的多少,给出经济实惠的选择建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简求值。
(1)已知x+y=15,x2+y2=113,求x2﹣xy+y2的值.
(2)先化简,再求值: ![]() ÷
÷ ![]() +1,在0,1,2,三个数中选一个合适的,代入求值.
+1,在0,1,2,三个数中选一个合适的,代入求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现:如图1,在△ABC中,∠C=90°,分别以AC,BC为边向外侧作正方形ACDE和正方形BCFG.
(1)△ABC和△DCF面积的关系是______________;(请在横线上填写“相等”或“不等”)
(2)拓展探究:若∠C≠90°,(1)中的结论还成立吗?若成立,请结合图2给出证明;若不成立,请说明理由;
(3)解决问题:如图3,在四边形ABCD中,AC⊥BD,且AC与BD的和为10,分别以四边形ABCD的四条边为边向外侧作正方形ABFE、正方形BCHG、正方形CDJI,正方形DALK,运用(2)的结论,图中阴影部分的面积和是否有最大值?如果有,请求出最大值,如果没有,请说明理由.
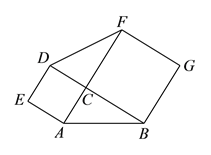
图1
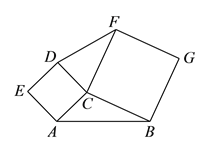
图2
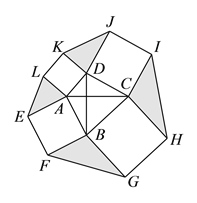
图3
查看答案和解析>>
科目:初中数学 来源: 题型:
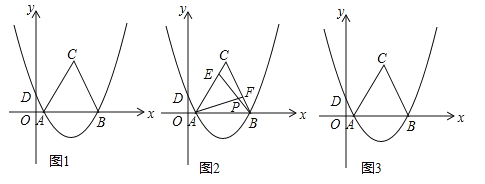
【题目】如图1,抛物线![]() ,经过A(1,0)、B(7,0)两点,交y轴于D点,以AB为边在x轴上方作等边△ABC.
,经过A(1,0)、B(7,0)两点,交y轴于D点,以AB为边在x轴上方作等边△ABC.
(1)求抛物线的解析式;
(2)在x轴上方的抛物线上是否存在点M,是S△ABM=![]() S△ABC?若存在,请求出点M的坐标;若不存在,请说明理由;
S△ABC?若存在,请求出点M的坐标;若不存在,请说明理由;
(3)如图2,E是线段AC上的动点,F是线段BC上的动点,AF与BE相交于点P.
①若CE=BF,试猜想AF与BE的数量关系及∠APB的度数,并说明理由;
②若AF=BE,当点E由A运动到C时,请直接写出点P经过的路径长(不需要写过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F. 
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60°,请你探究OE,EF之间有什么数量关系?并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com