
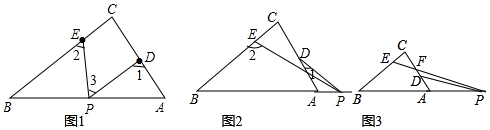
分析 (1)如图1中,结论:∠1+∠2=90°+∠3.连接AC,利用三角形的外角的性质证明即可;
(2)①如图2中,结论:∠2=90°+∠1+∠3.利用三角形的外角的性质证明即可;
②如图3中,结论:①中的结论不成立.结论:∠2=90°+∠1-∠3,证明方法类似;
解答 解:(1)如图1中,结论:∠1+∠2=90°+∠3.
理由:连接AC.
∵∠2=∠ECP+∠EPC,∠1=∠DCP+∠DPC,∠3=∠EPC+∠DPC,∠ACB=∠ECP+∠DCP=90°,
∴∠1+∠2=(∠ECP+∠DCP)+(∠EPC+∠DPC)=90°+∠3.
(2)①如图2中,结论:∠2=90°+∠1+∠3.
理由:∵∠2=∠C+∠CFE=90°+∠CFE,
又∵∠CFE=∠1+∠3,
∴∠2=90°+∠1+∠3.
②如图3中,结论:①中的结论不成立.结论:∠2=90°+∠1-∠3.
理由:∵∠2=∠C+∠CFE=90°+∠CFE,
又∵∠1=∠DFP+∠3,∠CFE=∠DFP,
∴∠CFE=∠1-∠3,
∴∠2=90°+∠1-∠3.
点评 此题是三角形综合题,主要考查了四边形的内角和,三角形的内角和,三角形的外角的性质,平角的定义,解本题的关键是将∠1,∠2,∠3转化到一个三角形或四边形中,是一道比较简单的中考常考题.


科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
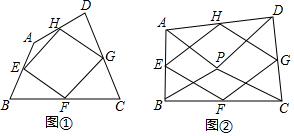
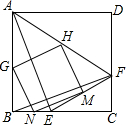 如图,在正方形ABCD中,点E,F分别在BC,CD边上,且BE=CF,连接AE,BF,EF、AF,点G、H、M、N分别是AB,AF,EF,BE的中点.
如图,在正方形ABCD中,点E,F分别在BC,CD边上,且BE=CF,连接AE,BF,EF、AF,点G、H、M、N分别是AB,AF,EF,BE的中点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y2>y1>y3 | D. | y3>y2>y1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{x-1}$ | B. | $\sqrt{x}$ | C. | $\sqrt{{x}^{2}+2}$ | D. | $\sqrt{{x}^{2}-2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ②④ | C. | ②⑤ | D. | ③⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
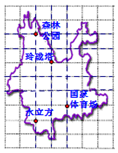 “健步走”越来越受到人们的喜爱,某个“健步走”小组将自己的活动场地定在奥林匹克公园,所走路线如图所示:森林公园-玲珑塔-国家体育场-水立方.设在奥林匹克公园设计图上玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),那么,水立方的坐标为( )
“健步走”越来越受到人们的喜爱,某个“健步走”小组将自己的活动场地定在奥林匹克公园,所走路线如图所示:森林公园-玲珑塔-国家体育场-水立方.设在奥林匹克公园设计图上玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),那么,水立方的坐标为( )| A. | (-2,-4) | B. | (-1,-4) | C. | (-2,4) | D. | (-4,-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com