
 如图,平行四边形ABCD的顶点A(-12,0),B(0,9),C(0,$\frac{21}{4}$),抛物线y=ax2+bx+c经过点A、B.
如图,平行四边形ABCD的顶点A(-12,0),B(0,9),C(0,$\frac{21}{4}$),抛物线y=ax2+bx+c经过点A、B.分析 (1)根据平行四边形性质即可求解.
(2)根据关于x的方程ax2+bx+c-$\frac{21}{4}$=$\frac{3}{4}$x有且只有一个解,利用判别式△=0求出a即可.
(3)方法一:如图所示,在直线AB上方作等腰直角三角形△ABE,EN⊥y轴,垂足为N,以AE中点M为圆心AM为半径画圆交直线CD于11,Q2,可以证明点Q11,Q2就是满足条件的QQ,再利用MA=MQ列出方程解决.
方法二;利用旋转法,求出点H坐标,再根据kQB=kBH列出方程求解.
解答 解:(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵OB=9,OC=$\frac{21}{4}$,
∴AD=BC=9-$\frac{21}{4}$=$\frac{15}{4}$,
∴点D坐标为(-12,-$\frac{15}{4}$).
(2)∵抛物线经过点A、B.
∴$\left\{\begin{array}{l}{144a-12b+c=0}\\{c=9}\end{array}\right.$,
∴b=$\frac{48a+3}{4}$,
由ax2+$\frac{48a+3}{4}$x+9-$\frac{21}{4}$=$\frac{3}{4}$x,整理得:4ax2+48ax+15=0,
∵此方程有且只有一个解,
∴△=0,
∴(48a)2-16a×15=0,
∴a=$\frac{5}{48}$(或0不合题意舍弃),
∴抛物线表达式为y=$\frac{5}{48}$x2+2x+9.
(3)如图所示,在直线AB上方作等腰直角三角形△ABE,EN⊥y轴,垂足为N,以AE中点M为圆心AM为半径画圆交直线CD于Q1,Q2,
∵∠AEB=45°,∠AEB+∠AQ1B=180°,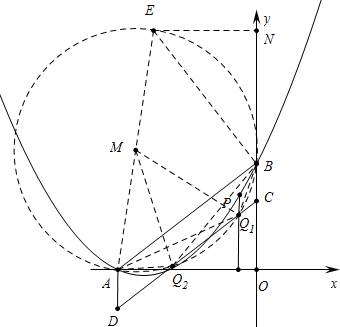
∴∠AQ1B=135°,
∴∠AQ1D+∠BQ1C=45°,
∴点Q1符合条件,同理点Q2也符合条件,
∵∠EBN+∠ABO=90°,∠ABO+∠BAO=90°,
∴∠BAO=∠EBN,
在△EBN和△BAO中,
$\left\{\begin{array}{l}{∠ENB=∠AOB=90°}\\{∠EBN=∠BAO}\\{EB=AB}\end{array}\right.$,
∴△EBN≌△BAO,
∴BN=AO=12,EN=BO=9,
∴点E(-9,21),点M(-$\frac{21}{2}$,$\frac{21}{2}$),
∵直线CD为y=$\frac{3}{4}$x+$\frac{21}{4}$,
设点P的横坐标为m,则点Q1(m,$\frac{3}{4}$m+$\frac{21}{4}$),
由AM=MQ1得到:($\frac{15\sqrt{2}}{2}$)2=(m+$\frac{21}{2}$)2+($\frac{3}{4}$m-$\frac{21}{4}$)2,
整理得:5m2+42m+81=0解得m=-3或-$\frac{27}{5}$,
故P点横坐标为-3或-$\frac{27}{5}$.
附(3)方法二:过点A作BQ垂线交BQ的延长线于H(见下图),设点P横坐标为t,则Q(t,$\frac{3}{4}t+\frac{21}{4}$),
∵∠AQD=45°-∠BQC,
∴∠AQH=45°
∴△AQH是等腰直角三角形,
∴点Q可以视为的A绕点H顺时针旋转90°而成,设H(m,n),
将点H平移至原点H′(0,0),则A′(-12-m,-n),
将A′绕原点顺时针旋转90°得Q′(-n,12+m)
则Q平移前坐标(m-n,12+m+n),
∴m-n=t,12+m+n=$\frac{3}{4}$t+$\frac{21}{4}$,
∴m=$\frac{7t-27}{8}$,n=$\frac{-t-27}{8}$,
∴点H($\frac{7t-27}{8}$,$\frac{-t-27}{8}$),
∵点H、点Q、点B共线,
∴kQB=kBH,
∴$\frac{\frac{3}{4}t+\frac{21}{4}-9}{t-0}=\frac{\frac{-t-27}{8}-9}{\frac{7t-27}{8}-0}$,
整理得到:5t2+42t+81=0,
∴t=-3或-$\frac{27}{5}$.
故点P横坐标为-3或-$\frac{27}{5}$.
点评 本题考查二次函数、一次函数的有关知识、平行四边形的性质、等腰直角三角形等知识,综合性比较强,通过45度角想到等腰直角三角形添加了辅助线是解题的关键.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:解答题
 有理数a,b,c在数轴上的位置如图所示.
有理数a,b,c在数轴上的位置如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 提炼方式 | 每天可提炼原材料的吨数 | 提炼率 | 提炼后所得产品的售价(元/吨) | 每提炼1吨原材料消耗的成本(元) |
| 粗提炼 | 7 | 90% | 30000 | 1000 |
| 精提炼 | 3 | 60% | 90000 | 3000 |
| 提炼厂利润 | 不超过150万元的部分 | 超过150万元但不超过200万元的部分 | 超过200万元的部分 |
| 提成比例 | 8% | a% | 15% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=2x-1 | B. | y=$\frac{1}{{x}^{2}}+3$ | C. | y=x2+2x-3 | D. | y=$\frac{5}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC内接于⊙O,且AB=AC,BO线与⊙O相交于点D,⊙O的切线AE交CD的延长线于点E,连接AD.
如图,已知△ABC内接于⊙O,且AB=AC,BO线与⊙O相交于点D,⊙O的切线AE交CD的延长线于点E,连接AD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com