
分析 先求出不等式组的解集,即可得出关于m、n的方程组,求出m、n即可.
解答 解:$\left\{\begin{array}{l}{2x-m<4①}\\{3x-2m≥n②}\end{array}\right.$
∵解不等式①得:x<$\frac{4+m}{2}$,
解不等式②得:x≥$\frac{n+2m}{3}$,
∴不等式组的解集为:$\frac{n+2m}{3}$≤x<$\frac{4+n}{2}$,
又∵关于x的不等式组$\left\{\begin{array}{l}{2x-m<4}\\{3x-2m≥n}\end{array}\right.$ 的解集是-2≤x<3,
∴$\left\{\begin{array}{l}{\frac{n+2m}{3}=-2}\\{\frac{4+n}{2}=3}\end{array}\right.$,
解得:m=-4,n=2,
∴(m+n)2=(-2)2=4.
点评 本题考查了解二元一次方程组和解一元一次不等式组,能得出关于m、n的方程组是解此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABC中,AB=AC,∠BAC=90°,在CB的延长线上取一点D,连接AD,过点A作AE⊥AD,过点C作CE⊥CB,AE与CE交于点E,连接BE,延长△ADC的中线AF交BE于点G.
如图,△ABC中,AB=AC,∠BAC=90°,在CB的延长线上取一点D,连接AD,过点A作AE⊥AD,过点C作CE⊥CB,AE与CE交于点E,连接BE,延长△ADC的中线AF交BE于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
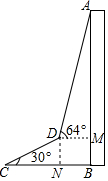 为了测量出大楼AB的高度,从距离楼底B处50米的点C(点C与楼底B在同一水平面上)出发,沿倾斜角为30°的斜坡CD前进20米到达点D,在点D处测得楼顶A的仰角为64°,求大楼AB的高度(结果精确到1米)(参考数据:sin64°≈0.9,cos64°≈0.4,tan64°≈2.1,$\sqrt{3}$≈1.7)
为了测量出大楼AB的高度,从距离楼底B处50米的点C(点C与楼底B在同一水平面上)出发,沿倾斜角为30°的斜坡CD前进20米到达点D,在点D处测得楼顶A的仰角为64°,求大楼AB的高度(结果精确到1米)(参考数据:sin64°≈0.9,cos64°≈0.4,tan64°≈2.1,$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
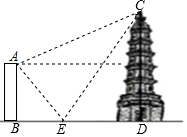 如图.大楼AB高16米,远处有一塔CD,某人在楼与塔间的平地E处测得塔顶的仰角为60°,楼顶的仰角为45°,爬到楼顶A处测得塔顶的仰角为30°,求塔CD的高度及大楼与塔之间的距离BD的长度.(结果精确到0.1米,参考数据:$\sqrt{2}≈$1.41,$\sqrt{3}≈$1.73)
如图.大楼AB高16米,远处有一塔CD,某人在楼与塔间的平地E处测得塔顶的仰角为60°,楼顶的仰角为45°,爬到楼顶A处测得塔顶的仰角为30°,求塔CD的高度及大楼与塔之间的距离BD的长度.(结果精确到0.1米,参考数据:$\sqrt{2}≈$1.41,$\sqrt{3}≈$1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com