
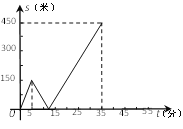
【题目】甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距![]() (米),甲行走的时间为
(米),甲行走的时间为![]() (分),
(分),![]() 关于
关于![]() 的函数函数图像的一部分如图所示.
的函数函数图像的一部分如图所示.
(1)求甲行走的速度;
(2)在坐标系中,补画![]() 关于
关于![]() 函数图象的其余部分;
函数图象的其余部分;
(3)问甲、乙两人何时相距360米?
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+2x+c的图象与x轴交于点A(3,0)和点C,与y轴交于点B(0,3).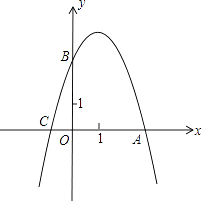
(1)求抛物线的解析式;
(2)在抛物线的对称轴上找一点D,使得点D到点B、C的距离之和最小,并求出点D的坐标解:;
(3)在第一象限的抛物线上,是否存在一点P,使得△ABP的面积最大?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
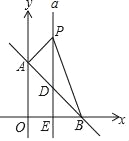
【题目】如图,平面直角坐标系中,直线AB:y=﹣x+b交y轴于点A,交x轴于点B,S△AOB=8.
(1)求点B的坐标和直线AB的函数表达式;
(2)直线a垂直平分OB交AB于点D,交x轴于点E,点P是直线a上一动点,且在点D的上方,设点P的纵坐标为m.
①用含m的代数式表示△ABP的面积;
②当S△ABP=6时,求点P的坐标;
③在②的条件下,在坐标轴上,是否存在一点Q,使得△ABQ与△ABP面积相等?若存在,直接写出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一台自动测温仪记录的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )

A. 凌晨4时气温最低为-3℃
B. 14时气温最高为8℃
C. 从0时至14时,气温随时间增长而上升
D. 从14时至24时,气温随时间增长而下降
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:
①△BDF≌△DCE;②∠BMD=120°;③△AMH是等边三角形;④S四边形ABMD= ![]() AM2 .
AM2 .
其中正确结论的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN为⊙O的直径,A、B是⊙O上的两点,过A作AC⊥MN于点C,过B作BD⊥MN于点D,P为DC上的任意一点,若MN=20,AC=8,BD=6,则PA+PB的最小值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,两个大小不同的球在水平面上靠在一起,组成如图所示的几何体,则该几何体的左视图是( ) 
A.两个内切的圆
B.两个外切的圆
C.两个相交的圆
D.两个外离的圆
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 从n边形的一个顶点出发,分别连接这个顶点和其余不相邻的各顶点,可以把这个n边形分成(n-3)个三角形
B. 当9:30时,时针和分针的小于平角的夹角是105°
C. 一个圆被三条半径分成面积比为3∶4∶5的三个扇形,则最小扇形的圆心角为90°
D. 19.38°=19°22′48″
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com