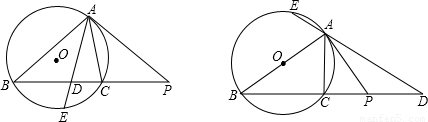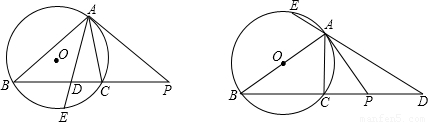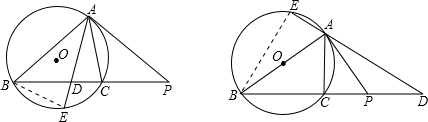
(1)证明:∵PA是⊙O的切线,
∴∠PAC=∠ABC,PA
2=PC•PB
∵PD
2=PB•PC
∴PA=PD
∴∠PAD=∠PDA
∴∠PAC+∠DAC=∠ABC+∠BAE
∵∠PAC=∠ABC
∴∠DAC=∠BAE
∴AD平分∠BAC;
(2)证明:连接BE,则∠AEB=∠ACB
∵∠BAE=∠CAD
∴△ABE∽△ADC
∴

=

即:AB•AC=AD•AE;
(3)解:(2)的结论仍然成立,
证明:连接BE
∵AB是直径
∴∠AEB=∠ACB=∠ACD=90°
∵PA是⊙O的切线
∴PA
2=PC•PB,∠BAP=90°
∵PD
2=PB•PC
∴PA=PD
∴∠PAD=∠PDA
∵∠BAP=90°,∠BEA=90°
∴∠BAE+∠PAD=∠BAE+∠EBA=90°
∴∠PAD=∠EBA
∵∠BEA=∠ACD=90°
∴△ABE∽△ADC
∴

=

,即:AB•AC=AD•AE
因此,(2)的结论仍然成立.
分析:(1)本题可先根据切割线定理,以及给出的PD
2=PB•PC,得出PA=PD,根据等边对等角,得出∠PAD=∠PDA,根据∠PAD=∠PAC+∠DAC,∠PDA=∠ABC+BAE,以及圆周角定理得出∠BAE=∠EAC,即AD平分∠BAC;
(2)本题实际求的是三角形ACD和ABE相似,已知的条件有:圆周角∠ACD=∠AEB,又由(1)的角平分线得出的∠BAE=∠CAE,因此两三角形就相似,即可得出题中所求证得结论;
(3)和(1)(2)的方法一样,先根据切割线定理得出PA=PD,然后根据等角的余角相等,得出∠EBA=∠PAD=∠D,又已知了一组直角,那么三角形ABE和三角形ACD相似,由此可得出所求的结论.
点评:本题主要考查了切线的性质,切割线定理以及相似三角形的判定与性质等知识点.用相似三角形来求线段的比例关系是本题的基本思路.

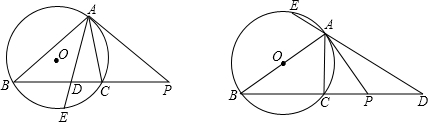
 (1)证明:∵PA是⊙O的切线,
(1)证明:∵PA是⊙O的切线, =
= 即:AB•AC=AD•AE;
即:AB•AC=AD•AE; =
= ,即:AB•AC=AD•AE
,即:AB•AC=AD•AE

 口算能手系列答案
口算能手系列答案