
��ͼ������������0��̶������MON�Ķ���O���룬��OM���þ���70��̶��ߴ���A�㣬��ON���þ���130��̶��ߴ���B�㣬���MON�Ĵ�С�ǣ�������

A. 20�� B. 30�� C. 40�� D. 60��
B �������������������ͼ�����Բ��������Բ��ΪC������AC��BC�� �߱�OM���þ���70��̶��ߴ���A�㣬 ���AOC����180�㣭70�㣩��55�㣬 �߱�ON���þ���130��̶��ߴ���B�㣬 ���BOC����180�㣭130�㣩��25�㣬 ���MON����AOC����BOC��55�㣭25�㣽30�㣮 ��ѡB�� ���ſ����ϵ�д�
���ſ����ϵ�д� ���Ŀ����ϵ�д�
���Ŀ����ϵ�д� ������ӱ������ͯ������ϵ�д�
������ӱ������ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2018�˽̰���꼶��ѧ�²���ϰ����ʮ���´����� ���ͣ���ѡ��
��ͼ���ڡ�ABC�У���C=90�㣬AC=2����D��BC�ϣ���ADC=2��B��AD= ����BC�ij�Ϊ�� ��
����BC�ij��� ��

A.  B.
B.  C.
C. 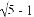 D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�걱ʦ������꼶��ѧ�ϲ��5�� һԪһ�η��� ��Ԫ���Ծ� ���ͣ������
�������㡰&����a&b��2a��b��������x&(x��6)��0��x��ֵΪ________��
2 �����������������x& (x��6)=0 2x+(x-6)=0 3x=6 x=2�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ������Т����2016-2017ѧ����꼶���ϣ���ĩ������ѧ�Ծ� ���ͣ������
�Ķ����в��ϣ������Ӧѧϰ����
�ĵ㹲Բ������
����֪����������һ�������ε�������������һ��Բ��������һ���ı��ε��ĸ���������һ��Բ��С������ʵ��̽�����֣����Խǻ������ı��ε��ĸ���������һ��Բ��������С�����÷�֤��֤����������Ĺ��̣�
��֪�����ı���ABCD�У���B+��D=180�㣮
��֤������A��B��C��D����һ��Բ��
֤������ͼ��1�����������A��B��C��D�ĵ㲻����һ��Բ����A��B��C������Բ������D��Բ�⣬��AD��Բ�ཻ�ڵ�E������CE������B+��AEC=180��������֪��B+��D=180�㣬���ԡ�AEC=��D������AEC�ǡ�CED����ǣ���AEC����D������ì�ܣ��ʼ��費��������˵�D�ڹ�A��B��C�����Բ�ϣ�
��ͼ��2���������A��B��C��D�ĵ㲻����һ��Բ����A��B��C������Բ������D��Բ�ڣ���AD���ӳ�����Բ�ཻ�ڵ�E������CE������B+��AEC=180��������֪��B+��ADC=180�㣬���ԡ�AEC=��ADC������ADC�ǡ�CED����ǣ���ADC����AEC������ì�ܣ��ʼ��費��������˵�D�ڹ�A��B��C�����Բ�ϣ�
��˵õ��ĵ㹲Բ�����������Խǻ������ı��ε��ĸ���������һ��Բ��
ѧϰ����
��1�������л��߲��ֽ��۵��������� ����
��2��֤����������Ҫ����������������ѧ˼�룺�� ��������ĸ���ż��ɣ�
A������˼�� B������˼�� C�����ν��˼�� D����������˼��
��3����ͼ��3�������ı���ABCD�У���ABC=��ADC=90�㣬��CAD=16�㣮AD=BD�������ADB�Ĵ�С��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ������Т����2016-2017ѧ����꼶���ϣ���ĩ������ѧ�Ծ� ���ͣ������
��ͼ��ʾ���صĵ�ѹΪ��ֵ��ʹ�ø�����ʱ������I����λ��A�������R����λ�������Ƿ�����������ϵ������ͼ����ͼ��ʾ������Դ�����Ϊ��Դ�ĵ��������Ƶ���������12A����ô�õ����ɱ����RӦ���Ƶķ�Χ��_____��
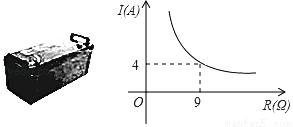
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ������Т����2016-2017ѧ����꼶���ϣ���ĩ������ѧ�Ծ� ���ͣ���ѡ��
��֪����������y= ��������������ͼ�����ڵ�ÿһ�������ڣ�y��ֵ����x�������������ôk��ȡֵ�����ǣ�������
��������������ͼ�����ڵ�ÿһ�������ڣ�y��ֵ����x�������������ôk��ȡֵ�����ǣ�������
A. 0 B. 2 C. 3 D. 4
A ������������������߷���������y����������������ͼ�����ڵ�ÿһ�������ڣ�y��ֵ����x����������� ��k��1��0�� ��k��1������k���ܵ�ȡֵֻ����0�� ��ѡA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�������ʡ�����жŶ������ؾ��꼶���ϣ���ĩ��ѧ�Ծ�������ѧ�ƣ� ���ͣ������
��ͼ����ֱ֪��y=��2x+12�ֱ���y�ᣬx�ύ��A��B���㣬��M��y���ϣ��Ե�MΪԲ�ĵġ�M��ֱ��AB�����ڵ�D������MD��
��1����֤����ADM�ס�AOB��
��2�������M�İ뾶Ϊ2 ����д����M�����꣬��д���ԣ���
����д����M�����꣬��д���ԣ��� ��
��  ��Ϊ���㣬�ҹ���M�������ߵĽ���ʽ��
��Ϊ���㣬�ҹ���M�������ߵĽ���ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�������ʡ�����жŶ������ؾ��꼶���ϣ���ĩ��ѧ�Ծ�������ѧ�ƣ� ���ͣ���ѡ��
����˵��������ǣ��� ����
A. ֱ����Բ������� B. ������ȵ��������ǵȻ�
C. �����ȵ�����Բ�ǵ�Բ D. �뾶��ȵ�������Բ�ǵȻ�
B �����������������A��ֱ����Բ������ң�����Aѡ���˵����ȷ�� B����ͬԲ���Բ�У�������ȵ��������ǵȻ�������Bѡ���˵������ C�������ȵ�����Բ�İ뾶��ȣ��������ǵ�Բ������Cѡ���˵����ȷ�� D���뾶��ȵ�������Բ�ǵȻ�������Dѡ���˵����ȷ�� ��ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ���ݵ���2017-2018ѧ��ȵ�һѧ����ĩ�����꼶��ѧ�Ծ� ���ͣ���ѡ��
��ͼ,��֪��ABE�ա�ACD,����ѡ���в��ܱ�֤���ĵ�ʽ��( )

A. AD=AE B. DB=AE C. DF=EF D. DB=EC
B ������������������ߡ�ABE�ա�ACD�� ��AB=AC��AD=AE����B=��C����A��ȷ�� ��AB-AD=AC-AE����BD=EC����D��ȷ�� �ڡ�BDF�͡�CEF�� ���BDF�ա�CEF��ASA���� ��DF=EF����C��ȷ�� ��ѡB���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com