
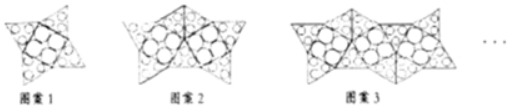
分析 观察给定图案,找出变化规律“每个图案比前一个图案多一个正方形、三个三角形”.
(1)由图案3中正方形及三角形的个数结合变化规律可找出图案4中正方形及三角形的个数,再结合每个正方形造型需要4盆A种菊花、每个三角形造型需要3盆B种菊花即可求出结论;
(2)根据图案n中三角形的个数结合B种菊花的盆数即可得出关于n的一元一次方程,解之即可得出结论;
(3)假设可以,设该处的两个图案分别为图案m和图案(m+1),根据图案变化规律结合A、B两种菊花盆数间的关系即可得出关于m的一元一次方程,解之即可得出m的值,由m为正整数即可得出假设成立.
解答 解:观察图形可知:每个图案比前一个图案多一个正方形、三个三角形.
(1)∵图案3由3个正方形、10个三角形构成,
∴图案4由4个正方形、13个三角形构成.
∵4×4=16,3×13=39,
∴图案4需要A种菊花16盆,需要B种菊花39盆.
(2)∵图案n中现有B种菊花75盆,
∴3×[4+3(n-1)]=75,
解得:n=8.
(3)假设可以,设该处的两个图案分别为图案m和图案(m+1),
根据题意得:3×[4+3(m-1)+4+3(m+1-1)]=2×4[m+(m+1)]+15,
解得:m=4,
∵4为正整数,
∴假设成立.
即该出图案可组成一副新作品.
点评 本题考查了规律型中图形的变化类以及一元一次方程的应用,解题的关键是:(1)根据图形的变化找出变化规律;(2)根据变化规律找出关于n的一元一次方程;(3)根据变形规律找出关于m的一元一次方程.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
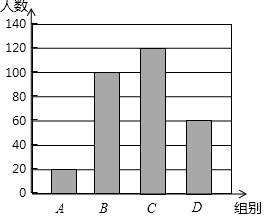 国家规定,中、小学生每天在校体育活动时间不低于1h,为此,某市就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图如图所示,其中A组为t<0.5h,B组为0.5h≤t<1h,C组为1h≤t<1.5h,D组为t≥1.5h.根据上述信息解答下列问题:
国家规定,中、小学生每天在校体育活动时间不低于1h,为此,某市就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图如图所示,其中A组为t<0.5h,B组为0.5h≤t<1h,C组为1h≤t<1.5h,D组为t≥1.5h.根据上述信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
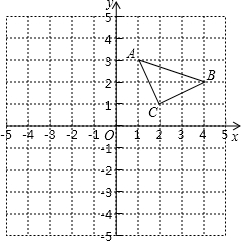 如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(1,3),B(4,2),C(2,1).
如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(1,3),B(4,2),C(2,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
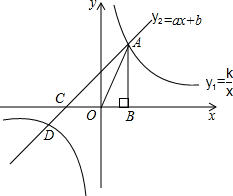 如图,已知反比例函数${y_1}=\frac{k}{x}$和一次函数y2=ax+b的图象相交于点A和点D,且点A的横坐标为1,点D的纵坐标为-1.过点A作AB⊥x轴于点B,△AOB的面积为1.求反比例函数和一次函数的解析式.
如图,已知反比例函数${y_1}=\frac{k}{x}$和一次函数y2=ax+b的图象相交于点A和点D,且点A的横坐标为1,点D的纵坐标为-1.过点A作AB⊥x轴于点B,△AOB的面积为1.求反比例函数和一次函数的解析式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com