
��1��2����3�������У������ȡ��������ˣ����������ĸ����� ��
�� ��������������������ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ���������ȡ��������ˣ���������������������ø��ʹ�ʽ��⼴����ô𰸣� �������� ����״ͼ�ã� �߹���6�ֵȿ��ܵĽ���������ȡ��������ˣ�������������2������� �������ȡ��������ˣ����������ĸ����ǣ�=�� �ʴ�Ϊ����
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���˽̰���꼶�꼶��ѧ�²�ڶ�ʮ���� ������ ���ͣ���ѡ��
һ�������������ͼ��ͼ�����丩��ͼΪ�����Σ������������ı����Ϊ��������
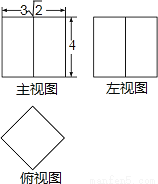
A. 66 B. 48 C. 48 +36 D. 57
+36 D. 57
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰����꼶�²���ѧ�������ཻ����ƽ���ߵ�Ԫ���� ���ͣ������
��ͼ��ʾ��ֱ��a��b��ֱ��c��ֱ��a��b�ֱ��ཻ�ڵ�A����B��AM��b������Ϊ��M������l=58�㣬���2= ___________ .
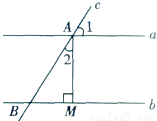
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰����꼶�²���ѧ�������ཻ����ƽ���ߵ�Ԫ���� ���ͣ���ѡ��
��ͼ�����������У���1����B+��BCD=180�㣻��2����1=��2����3����3=��4����4����B=��5�����ж�AB��CD�����������У� ��

A. 1 B. 2 C. 3 D. 4
C ���������������������ƽ���ߵ��ж���������1����3����4�����ж�AB��CD�� �������� ��1����B+��BCD=180�㣬ͬ���ڽǻ�������ֱ��ƽ�У������ж�AB��CD�� ��2����1=��2������1����2���ǽ�AB��CD���õ��ڴ��ǣ��������ж�AB��CD�� ��3����3=��4���ڴ�����ȣ���ֱ��ƽ�У������ж�AB��CD�� ��4����B=��5��ͬλ����ȣ���ֱ��ƽ�У�������...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ��ʦ����ϲ� ��3�� ���ʵĽ�һ����ʶ ��Ԫ���Ծ� ���ͣ������
����ʦ��1����������ɸ�����(��Щ�����ɫ�ⶼ��ͬ)����һ�������Ŀڴ������ȣ�������ѧ����������ʵ�飬ÿ������1����(�зŻ�)���±��ǻ�����е�һ��ͳ������.
����Ĵ���n | 100 | 150 | 200 | 500 | 800 | 1000 |
��������Ĵ���m | 23 | 31 | 60 | 130 | 203 | 251 |
���������Ƶ�� | 0.23 | 0.207 | 0.30 | 0.26 | 0.254 | 0.251 |
(1)�����ϱ����ݹ��ƴӴ�������1�����Ǻ���ĸ�����_________��
(2)���ƴ��а���ĸ�����
(1)0.25(2)���ƴ�����3������ �������������������1���ô����ظ��������¼�������Ƶ���ȶ���ij����������ʾ���¼������ĸ��ʼ��ɣ� ��2�����ø��ʹ�ʽ�г�������⼴�ɣ� �����������1��251��1000=0.251�� �ߴ����ظ������¼�������Ƶ�����ȶ���0.25������ ����ƴӴ�������һ�����Ǻ���ĸ�����0.25�� ��2������а���Ϊx���� =0....�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ��ʦ����ϲ� ��3�� ���ʵĽ�һ����ʶ ��Ԫ���Ծ� ���ͣ���ѡ��
��ͼ������ת���У�ָ������ÿһ�����ϵĻ�����ȣ���ô����ָ��ͬʱ����ż���ϵĸ����ǣ� ��

A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ��ʦ����ϲ� ��3�� ���ʵĽ�һ����ʶ ��Ԫ���Ծ� ���ͣ���ѡ��
����������ֱ�д�����֣�1��1��2�Ŀ�Ƭ�����DZ�����ȫ��ͬ���ֽ������ſ�Ƭ���泯��ϴ�Ⱥ������ȡһ�ţ���������������Ϊa��ֵ��Ȼ���ٴ�ʣ������ſ�Ƭ�����һ�ţ����������������Ϊb��ֵ�����(a��b)�ڵڶ����ĸ���Ϊ(����)
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ�˽̰��ϲ� ȫ���ۺϲ��Ծ� ���ͣ���ѡ��
��ͼ���ڡ�ABC�У�AB=AC����BAC=100�㣬AB�Ĵ�ֱƽ����DE�ֱ�AB��BC�ڵ�D��E�����BAE=�� ��
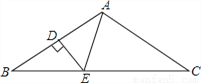
A. 80�� B. 60�� C. 50�� D. 40��
D ���������������������ε��ڽǺͶ����͵��������ε����ʡ�B�������߶δ�ֱƽ���ߵ�������AE=BE����BAE=��B�� �������� ��AB=AC����BAC=100�㣬���B=��C=��180�㩁100�㣩��2=40�㣬��DE��AB�Ĵ�ֱƽ���ߣ���AE=BE�����BAE=��B=40�㣬 ��ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�˽̰���꼶��ѧ�²���ϰ����ʮ���´����� ���ͣ������
һ��ֱ�����ǰ���ͼ���ã���C��FD���ӳ����ϣ�AB��CF����F=��ACB=90�㣬��E=45�㣬��A=60�㣬AC=10������CD�ij���
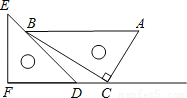
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com