
【题目】定义:对于给定的一次函数y=ax+b(a≠0),把形如![]() 的函数称为一次函数y=ax+b(a≠0)的衍生函数.已知矩形ABCD的顶点坐标分别为A(1,0),B(1,2),C(-3,2),D(-3,0).
的函数称为一次函数y=ax+b(a≠0)的衍生函数.已知矩形ABCD的顶点坐标分别为A(1,0),B(1,2),C(-3,2),D(-3,0).
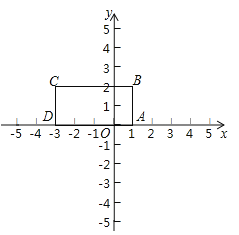
(1)已知函数y=2x+l.
①若点P(-1,m)在这个一次函数的衍生函数图像上,则m= .
②这个一次函数的衍生函数图像与矩形ABCD的边的交点坐标分别为 .
(2)当函数y=kx-3(k>0)的衍生函数的图象与矩形ABCD有2个交点时,k的取值范围是 .
【答案】(1)①3,②(![]() ,2)或(
,2)或(![]() ,,0);(2)1<k<3;
,,0);(2)1<k<3;
【解析】
(1)①x=-1<0,则m=-2×(-1)+1=3,即可求解;②一次函数的衍生函数图象与矩形ABCD的边的交点位置在BC和AD上,即可求解;
(2)当直线在位置①时,函数和矩形有1个交点,当直线在位置②时,函数和图象有3个交点,在图①②之间的位置,直线与矩形有2个交点,即可求解.
解:(1)①x=-1<0,则m=-2×(-1)+1=3,
故答案为:3;
②一次函数的衍生函数图象与矩形ABCD的边的交点位置在BC和AD上,
当y=2时,2x+1=2,解得:x=![]() ,
,
当y=0时,2x+1=0,解得:x=![]() ,
,
故答案为:(![]() ,2)或(
,2)或(![]() ,,0);
,,0);
(2)函数可以表示为:y=|k|x-3,
如图所示当直线在位置①时,函数和矩形有1个交点,

当x=3时,y=|k|x-3=3|k|-3=0,k=±1,
k>0,取k=1
当直线在位置②时,函数和图象有3个交点,
同理k=3,
故在图①②之间的位置,直线与矩形有2个交点,
即:1<k<3.


科目:初中数学 来源: 题型:
【题目】如图1,已知直线y=﹣2x+4与两坐标轴分别交于点A、B,点C为线段OA上一动点,连接BC,作BC的中垂线分别交OB、AB交于点D、E.
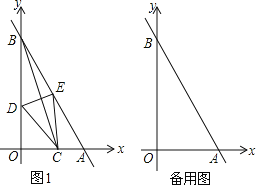
(l)当点C与点O重合时,DE= ;
(2)当CE∥OB时,证明此时四边形BDCE为菱形;
(3)在点C的运动过程中,直接写出OD的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
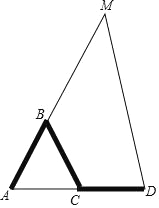
【题目】如图,AB﹣BC﹣CD是一根三节棍,其中线段AB、BC、CD首尾顺次相连,且AB=BC=CD,将这个三节棍摆放在△AMD中,使它的两个端点与△AMD两个顶点重合,三节棍的首尾两节在△AMD的边上,则AB﹣BC﹣CD就是△AMD的配套三节棍.
(1)若∠A=60°,AD=60,求△AMD的配套三节棍的总长;
(2)若AM=AD,△AMD的配套三节棍AB﹣BC﹣CD中一边BC平行于MD,利用直尺圆规画出图形,并求出∠A的度数.(保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若x=﹣m和x=m﹣4时,多项式ax2+bx+4a+1的值相等,且m≠2.当﹣1<x<2时,存在x的值,使多项式ax2+bx+4a+1的值为3,则a的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
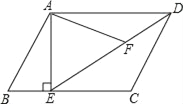
【题目】如图,平行四边形ABCD,AE⊥BC交点E,连接DE,F为DE上一点,且∠AFE=∠B=60°.
(1)求证:△ADF∽△DEC;
(2)若AE=3,AD=4,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
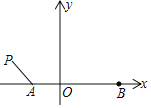
【题目】如图,在平面直角坐标系中,点A的坐标为(﹣1,0),点B的坐标为(2,0),点P为线段AB外一动点且PA=1,以PB为边作等边△PBM,则当线段AM的长取到最大值时,点P的横坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生每天的睡眠情况,某初中学校从全校 800 名学生中随机抽取了 40 名学生,调查了他们平均每天的睡眠时间(单位: h) ,统计结果如下:
9,8,10.5,7,9,8,10,9.5,8,9,9.5,7.5,9.5,9,8.5,7.5,10,9.5,8,9,
7,9.5,8.5,9,7,9,9,7.5,8.5,8.5,9,8,7.5,9.5,10,9.5,8.5,9,8,9.
在对这些数据整理后,绘制了如下的统计图表:
睡眠时间分组统计表 睡眠时间分布情况
组别 | 睡眠时间分组 | 人数(频数) |
1 | 7≤t<8 | m |
2 | 8≤t<9 | 11 |
3 | 9≤t<10 | n |
4 | 10≤t<11 | 4 |

请根据以上信息,解答下列问题:
(1) m = , n = , a = , b = ;
(2)抽取的这 40 名学生平均每天睡眠时间的中位数落在 组(填组别) ;
(3)如果按照学校要求,学生平均每天的睡眠时间应不少于 9 h,请估计该校学生中睡眠时间符合要求的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
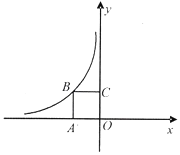
【题目】如图,正方形OABC的面积为4,点O为坐标原点,点B在函数y![]() (k<0,x<0)的图象上,点P(m,n)是函数y
(k<0,x<0)的图象上,点P(m,n)是函数y![]() (k<0,x<0)的图象上异于B的任意一点,过点P分别作x轴、y轴的垂线,垂足分别为E、F.
(k<0,x<0)的图象上异于B的任意一点,过点P分别作x轴、y轴的垂线,垂足分别为E、F.
(1)设矩形OEPF的面积为S1,求S1;
(2)从矩形OEPF的面积中减去其与正方形OABC重合的面积,剩余面积记为S2.写出S2与m的函数关系式,并标明m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com