
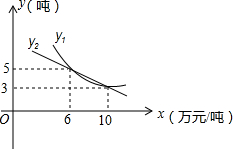
 今年某水果超市都以2万元/吨的价格购进甲、乙两种水果,甲水果的销量y1(吨)、乙水果的销量y2(吨)与售价x(万元/吨)之间大致满足如图所示的两个函数关系.
今年某水果超市都以2万元/吨的价格购进甲、乙两种水果,甲水果的销量y1(吨)、乙水果的销量y2(吨)与售价x(万元/吨)之间大致满足如图所示的两个函数关系.分析 (1)直接利用待定系数法求出函数解析式进而得出答案;
(2)利用函数图象得出x的取值范围;
(3)直接利用利润=销售量×(售价-进价),进而得出方程求出答案.
解答 解:(1)设y1=$\frac{k}{x}$,将(6,5)代入得:
k=30,
则y1的函数解析式为:y1=$\frac{30}{x}$,
设y2=ax+b,将(6,5),(10,3),
则$\left\{\begin{array}{l}{6a+b=5}\\{10a+b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=8}\end{array}\right.$,
故y2的函数解析式为:y2=-$\frac{1}{2}$x+8;
(2)如图所示:当0<x<6时或x>10时,甲水果的销量大于乙水果的销量;
(3)设甲的利润为:w1根据题意可得:
w1=(x-2)×$\frac{30}{x}$=30-$\frac{60}{x}$=12,
解得:x=$\frac{10}{3}$,
乙的利润为:w2根据题意可得:
w2=(x-2)×(-$\frac{1}{2}$x+8)=12,
解得:x1=4,x2=14,
答:甲种水果的售价定为$\frac{10}{3}$万元/吨时,能获得12万元的利润,
乙种水果的售价定为4或14万元/吨时,能获得12万元的利润.
点评 此题主要考查了反比例函数以及一次函数和一元二次方程的应用,正确得出函数关系式是解题关键.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:选择题
| A. | x-3 | B. | $\frac{1}{x}+1=0$ | C. | $2x=\frac{1}{3}$ | D. | 2x-3y=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8000(1+x)2=7000 | B. | 8000(1-x)2=7000 | C. | 7000(1-x)2=8000 | D. | 7000(1+x)2=8000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
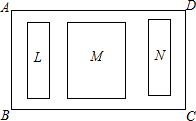 要对一块长60m.宽40m的矩形荒地ABCD(BC>AB)进行绿化和硬化,设计方案如图所示.矩形L、M、N为三块绿地.其余为硬化路面,L、M、N三块绿地周围的硬化路面宽都相等.并使三块绿地面积的和为矩形ABCD面积的$\frac{1}{2}$.
要对一块长60m.宽40m的矩形荒地ABCD(BC>AB)进行绿化和硬化,设计方案如图所示.矩形L、M、N为三块绿地.其余为硬化路面,L、M、N三块绿地周围的硬化路面宽都相等.并使三块绿地面积的和为矩形ABCD面积的$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,菱形ABCD的周长为8,对角线AC和BD相交于点O,AC:BD=1:2,则AO:BO=1:2,菱形ABCD的面积S=$\frac{16}{5}$.
如图,菱形ABCD的周长为8,对角线AC和BD相交于点O,AC:BD=1:2,则AO:BO=1:2,菱形ABCD的面积S=$\frac{16}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AB=A'B',AC=A'C,∠B=∠B' | B. | AB=A'B',BC=B'C,∠A=∠A' | ||
| C. | AC=A'C',BC=B'C',∠C=∠C' | D. | AC=A'C',BC=B'C',∠B=∠B' |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com