
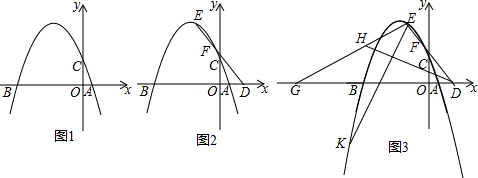
分析 (1)先根据函数关系式求出对称轴,由AB=10,求出点A的坐标,代入函数关系式求出c的值,即可解答;
(2)作EM⊥x轴,垂足为点M,FN⊥x轴,垂足为点N,FT⊥EM,垂足为点T.得到四边形FTMN为矩形,由EM∥FN,FT∥BD.得到∠BDE=∠EFT,所以tan∠EFT=$\frac{4}{3}$,
设E(-3m,yE),F(-m,yF),得到$\frac{4}{3}=\frac{{y}_{E}-{y}_{F}}{-m-(-3m)}$,再由yE-yF=$\frac{8}{3}m$=(-3m2+8m+3)-(-$\frac{1}{3}{m}^{2}+\frac{8}{3}m$+3),解得m=1,-3m=-3,代入函数关系式即可解答;
(3)作EM⊥x轴,垂足为点M,过点K作KR⊥ED,与ED相交于点R,与x轴相交于点Q.再证明△EGM≌△EKR,求出Q(-$\frac{1}{3}$,0),R($\frac{9}{5}$,$\frac{8}{5}$),从而得到直线RQ的解析式为:y=$\frac{3}{4}x+\frac{1}{4}$.设点K的坐标为(x,$\frac{3}{4}x+\frac{1}{4}$)代入抛物线解析式可得x=-11,即可解答.
解答 解:(1)由y=-$\frac{1}{3}$x2-$\frac{8}{3}$x+c,
可得对称轴为x=-4
∵AB=10,
∴点A的坐标为(1,0),
∴$-\frac{1}{3}×{1}^{2}-\frac{8}{3}×1+c=0$,
∴c=3
∴抛物线的解析式为y=-$\frac{1}{3}{x}^{2}-\frac{8}{3}x$+3.
(2)如图2,作EM⊥x轴,垂足为点M,FN⊥x轴,垂足为点N,FT⊥EM,垂足为点T.
∴∠TMN=∠FNM=∠MTF=90°,
∴四边形FTMN为矩形,
∴EM∥FN,FT∥BD.
∴∠BDE=∠EFT,
∵tan∠BDE=$\frac{4}{3}$,
∴tan∠EFT=$\frac{4}{3}$,
设E(-3m,yE),F(-m,yF)
∴$\frac{4}{3}=\frac{{y}_{E}-{y}_{F}}{-m-(-3m)}$
∵y=-$\frac{1}{3}{x}^{2}-\frac{8}{3}x$+3过点E、F,
则yE-yF=$\frac{8}{3}m$=(-3m2+8m+3)-(-$\frac{1}{3}{m}^{2}+\frac{8}{3}m$+3),
解得m=0(舍去)或m=1,
当m=1时,-3m=-3,
∴${y}_{E}=-\frac{1}{3}×(-3)^{2}-\frac{8}{3}×(-3)+3$=8.
∴E(-3,8).
(3)如图3,作EM⊥x轴,垂足为点M,过点K作KR⊥ED,与ED相交于点R,与x轴相交于点Q.
∵∠KER+∠EDH=90°,∠EGM+∠GEM=90°,∠EDH=∠EGM,
∴∠KER=∠GEM,
在△EGM和△EKR中,
$\left\{\begin{array}{l}{∠KER=∠GEM}\\{∠GME=∠KRE}\\{EK=EG}\end{array}\right.$
∴△EGM≌△EKR,
∴EM=ER=8,
∵tan∠BDE=$\frac{4}{3}$.
∴ED=10,
∴DR=2,
∴DQ=$\frac{10}{3}$
∴Q(-$\frac{1}{3}$,0),
可求R($\frac{9}{5}$,$\frac{8}{5}$)
∴直线RQ的解析式为:y=$\frac{3}{4}x+\frac{1}{4}$.
设点K的坐标为(x,$\frac{3}{4}x+\frac{1}{4}$)代入抛物线解析式可得x=-11
∴K(-11,-8).
点评 本题是二次函数的综合题,考查了二次函数的性质和二次函数图象上点的坐标特征,待定系数法求函数解析式,全等三角形的性质定理与判定定理,解决本题的关键是准确做出辅助线.


科目:初中数学 来源: 题型:填空题
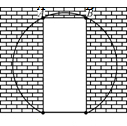 温州外国语学校在进行校园二次美化工程,一面墙上有一个矩形的门洞,如图,已知矩形的高为2米,宽为0.8米,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,圆弧所在的圆的半径长为$\frac{2\sqrt{29}}{5}$米.
温州外国语学校在进行校园二次美化工程,一面墙上有一个矩形的门洞,如图,已知矩形的高为2米,宽为0.8米,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,圆弧所在的圆的半径长为$\frac{2\sqrt{29}}{5}$米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
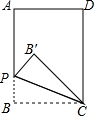 如图,在矩形ABCD中,AB=4,BC=3,点P是AB上(不含端点A,B)任意一点,把△PBC沿PC折叠,当点B′的对应点落在矩形ABCD的对角线上时,BP=$\frac{3}{2}$或$\frac{9}{4}$.
如图,在矩形ABCD中,AB=4,BC=3,点P是AB上(不含端点A,B)任意一点,把△PBC沿PC折叠,当点B′的对应点落在矩形ABCD的对角线上时,BP=$\frac{3}{2}$或$\frac{9}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
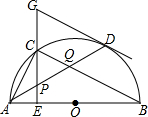 如图,AB是半圆O的直径,D是$\widehat{AB}$上一点,C是$\widehat{AD}$的中点,过点C作AB的垂线,交AB于E,与过点D的切线交于点G,连接AD,分别交CE、CB于点P、Q,连接AC,关于下列结论:
如图,AB是半圆O的直径,D是$\widehat{AB}$上一点,C是$\widehat{AD}$的中点,过点C作AB的垂线,交AB于E,与过点D的切线交于点G,连接AD,分别交CE、CB于点P、Q,连接AC,关于下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
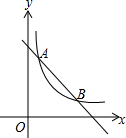 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A(6,1),B(a,6)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A(6,1),B(a,6)两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com