
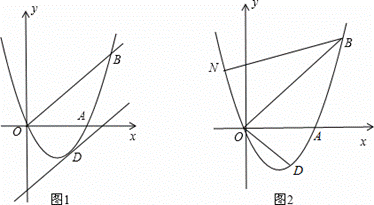
如图1,已知抛物线y=ax2+bx(a≠0)经过A(3,0)、B(4,4)两点.
(1)求抛物线的解析式;
(2)将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个公共点D,求m的值及点D的坐标;
(3)如图2,若点N在抛物线上,且∠NBO=∠ABO,则在(2)的条件下,求出所有满足
△POD∽△NOB的点P坐标(点P、O、D分别与点N、O、B对应).
 |
解:(1)∵抛物线y=ax2+bx(a≠0)经过A(3,0)、B(4,4)
∴将A与B两点坐标代入得: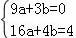 ,解得:
,解得: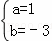 ,
,
∴抛物线的解析式是y=x2﹣3x.
(2)设直线OB的解析式为y=k1x,由点B(4,4),
得:4=4k1,解得:k1=1 ∴直线OB的解析式为y=x,
∴直线OB向下平移m个单位长度后的解析式为:y=x﹣m,
∴x﹣m=x2﹣3x,
 ∵抛物线与直线只有一个公共点, ∴△=16﹣4m=0,
∵抛物线与直线只有一个公共点, ∴△=16﹣4m=0,
解得:m=4,
此时x1=x2=2,y=x2﹣3x=﹣2,
∴D点的坐标为(2,﹣2).
(3)∵直线OB的解析式为y=x,且A(3,0),
∴点A关于直线OB的对称点A′的坐标是(0,3),
根据轴对称性质和三线合一性质得出∠A′BO=∠ABO,
设直线A′B的解析式为y=k2x+3,过点(4,4),
∴4k2+3=4,解得:k2=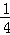 , ∴直线A′B的解析式是y=
, ∴直线A′B的解析式是y= ,
,
∵∠NBO=∠ABO,∠A′BO=∠ABO, ∴BA′和BN重合,即点N在直线A′B上,
∴设点N(n,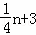 ),又点N在抛物线y=x2﹣3x上,
),又点N在抛物线y=x2﹣3x上,
∴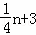 =n2﹣3n, 解得:n1=﹣
=n2﹣3n, 解得:n1=﹣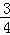 ,n2=4(不合题意,舍去)
,n2=4(不合题意,舍去)
∴N点的坐标为(﹣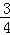 ,
,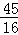 ).
).
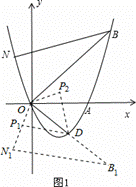
如图1,将△NOB沿x轴翻折,得到△N1OB1,
则N1(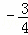 ,
, ),B1(4,﹣4),
),B1(4,﹣4),
∴O、D、B1都在直线y=﹣x上.
∵△P1OD∽△NOB,△NOB≌△N1OB1, ∴△P1OD∽△N1OB1,
∴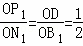 , ∴点P1的坐标为(
, ∴点P1的坐标为(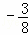 ,
,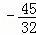 ).
).
将△OP1D沿直线y=﹣x翻折,可得另一个满足条件的点P2(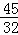 ,
,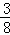 ),
),
综上所述,点P的坐标是( ,
,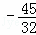 )或(
)或(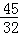 ,
,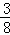 ).
).


科目:初中数学 来源: 题型:
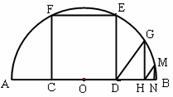
如图,AB是半圆O的直径,且AB=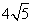 ,矩形CDEF内接于半圆,点C,D在AB上,点E,F在半圆上.
,矩形CDEF内接于半圆,点C,D在AB上,点E,F在半圆上.
(1)当矩形CDEF相邻两边FC︰CD=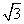 ︰2时,求弧AF的度数;
︰2时,求弧AF的度数;
(2)当四边形CDEF是正方形时:
①试求正方形CDEF的边长;
②若点G,M在⊙O上, GH⊥AB于H,MN⊥AB于N,且△GDH和△MHN都是等腰直角三角形,求HN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
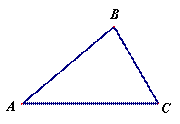
已知:如图,在△ABC中,∠A=40°,∠B=80°。
(1)作∠B的平分线BD,交AC于点D;作AB的中点E
(要求:尺规作图,保留作图痕迹,不必写作法和证明);
(2)连接DE,求证:△ADE≌△BDE。
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
已知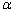 是某直角三角形内角中较大的锐角,
是某直角三角形内角中较大的锐角,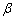 是某五边形的外角中的最大角,甲、乙、丙、丁计算
是某五边形的外角中的最大角,甲、乙、丙、丁计算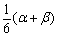 的结果依次为10°、15°、30°、35°,其中有正确的结果,则计算正确的是( )
的结果依次为10°、15°、30°、35°,其中有正确的结果,则计算正确的是( )
A.甲 B.乙 C.丙 D.丁
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com