
如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在C、D之间有一点P,如果P点在C、D之间运动时,问∠PAC,∠APB,∠PBD之间的关系是否发生变化.若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?


解: 若P点在C、D之间运动时,则有∠APB=∠PAC+∠PBD.
理由是:如图4,过点P作PE∥l1,则∠APE=∠PAC,
又因为l1∥l2,所以PE∥l2,所以∠BPE=∠PBD,
所以∠APE+∠BPE=∠PAC+∠PBD,即∠APB=∠PAC+∠PBD.
若点P在C、D两点的外侧运动时(P点与点C、D不重合),则有两种情形:
(1)如图1,有结论:∠APB=∠PBD-∠PAC.
理由是:过点P作PE∥l1,则∠APE=∠PAC,
又因为l1∥l2,所以PE∥l2,所以∠BPE=∠PBD,
所以∠APB=∠BAE+∠APE,即∠APB=∠PBD-∠PAC.
(2)如图2,有结论:∠APB=∠PAC-∠PBD.
理由是:过点P作PE∥l2,则∠BPE=∠PBD,
又因为l1∥l2,所以PE∥l1,所以∠APE=∠PAC,
所以∠APB=∠APE+∠BPE,即∠APB=∠PAC+∠PBD.






科目:初中数学 来源: 题型:
如图4,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
A.30° B.25° C.20° D.15°

查看答案和解析>>
科目:初中数学 来源: 题型:
已知三条不同的直线a,b,c在同一平面内,下列四个命题:
①如果a∥b,a⊥c,那么b⊥c; ②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c; ④如果b⊥a,c⊥a,那么b∥c.
其中真命题的是 .(填写所有真命题的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
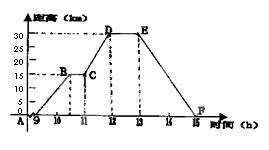
25.小强骑自行车去郊游,9点离开家以 千米/小时的速度匀速行驶到
千米/小时的速度匀速行驶到
B地,15点回到家,如下图是他离家的距离y(千米)与所对应时间x(小时)之间关系的函数图象 ,
,
根据这个 图象,请你回答下列问题:
图象,请你回答下列问题:
(1)小强到离家最远的地方用了几小时?此时离家多远?
(2)计算求出何时开始第一次休息?休息时间多长?
(3)小强何时距家21km?(写出计算过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com