
分析 首先把a2+b2+c2-ab-bc-ac两两结合为a2-ab+b2-bc+c2-ac,利用提取公因式法因式分解,再把a、b、c代入求值即可.
解答 解:a2+b2+c2-ab-bc-ac
=a2-ab+b2-bc+c2-ac
=a(a-b)+b(b-c)+c(c-a),
当a=2011x+2010,b=2011x+2011,c=2011x+2012时,
原式=(2011x+2010)×(-1)+(2011x+2011)×(-1)+(2011x+2012)×2
=-2011x-2010-2011x-2011+2011x×2+2012×2
=3.
点评 此题利用因式分解求代数式求值,注意代数之中字母之间的联系,正确运用因式分解,巧妙解答题目.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案科目:初中数学 来源: 题型:解答题
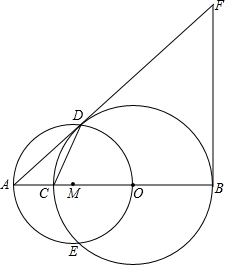 如图,C为线段AB上一点,以BC为直径作⊙O,再以AO为直径作⊙M交⊙O于D、E,过点B作AB的垂线交AD的延长线于F,连结CD.
如图,C为线段AB上一点,以BC为直径作⊙O,再以AO为直径作⊙M交⊙O于D、E,过点B作AB的垂线交AD的延长线于F,连结CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2+2x-3=0 | B. | x2+x+$\frac{1}{4}$=0 | C. | x2+$\sqrt{2}$x+1=0 | D. | -x2+3=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com