
| 年份 | 全国人口 (亿人) | 儿童人口 (亿人) | 儿科医生 (万人) | 每千名儿童拥有的儿科医生数 |
| 2000 | 12.67 | 2.9 | 9.57 | 0.33 |
| 2005 | 13.06 | 2.65 | 10.07 | 0.38 |
| 2010 | 13.4 | 2.22 | 10.43 | 0.47 |
| 2015 | 13.7 | 2.26 | 9.72 | 0.43 |
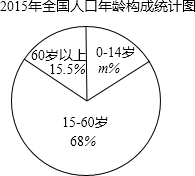
分析 (1)根据扇形统计图可以得到m的值;
(2)根据表格中的数据可以预测2020的人口数;
(3)根据第(2)问的人口数可以求得儿科医生增加的人数.
解答 解:(1)m%=1-15.5%-68%=16.5%,
即扇形统计图中m的值是16.5;
(2)2000年至2005年人口增加13.06-12.67=0.39亿人,
2005至2010年人口增加13.4-13.06=0.34亿人,
2010年至2015年人口增加13.7-13.4=0.3亿人,
由此可知每5年人口的增加数量逐渐稳定到0.3亿左右,
故预测2015-2020增加的人口数为0.3亿,即14亿,
故答案为:14;
(3)设到2020年我国儿科医生需比2015年增加x万人,才能使每千名儿童拥有的儿科医生数达到0.6,
(9.72+x)÷[14×$\frac{2.26}{13.7}$×10000÷1000]=0.6,
解得,x≈4.14
即到2020年我国儿科医生需比2015年增加4.14万人,才能使每千名儿童拥有的儿科医生数达到0.6.
点评 本题考查扇形统计图和用样本估计总体,解题的关键是明确题意,找出所求问题需要的条件.


科目:初中数学 来源: 题型:选择题
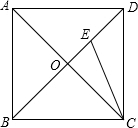 如图,正方形ABCD的两条对角线AC,BD相交于点O,点E在BD上,且BE=CD,则∠BEC的度数为( )
如图,正方形ABCD的两条对角线AC,BD相交于点O,点E在BD上,且BE=CD,则∠BEC的度数为( )| A. | 22.5° | B. | 60° | C. | 67.5° | D. | 75° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC和△DBE中,AB=CB,DB=EB,∠ABC=∠DBE=50°.若∠BDC=25°,AD=4,DE=$\sqrt{13}$,则CD的长为( )
如图,△ABC和△DBE中,AB=CB,DB=EB,∠ABC=∠DBE=50°.若∠BDC=25°,AD=4,DE=$\sqrt{13}$,则CD的长为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{13}}{2}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 100$\sqrt{3}$米 | B. | 200米 | C. | 300米 | D. | 500米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com