
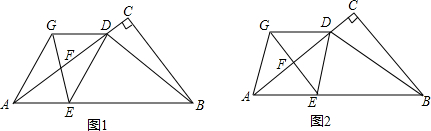
���� ��1�����ݶԽ�����ƽ�ֵ��ı�����ƽ���ı����ж���
��2�����ı���GEBD��ƽ���ı��Σ��õ�GE��BD������ƽ���ߵȷ��߶ζ����õ������
��3�����ݶԽ����ഹֱ��ƽ���ı���������֤�ã�����ƽ���߷��߶γɱ����з�����⣮
��� �⣺��1��֤������DG��AE��
���G=��AE��G����GDF=��A��
�ڡ�GFD���AFE�У�$\left\{\begin{array}{l}{��G=��AEG}\\{��GDF=��A}\\{DF=AF}\end{array}\right.$��
���GFD�ա�AFE��
��GF=EF��
��DF=AF��
���ı���GAEF��ƽ���ı��Σ�
��2�����ı���GEBD��ƽ���ı���ʱ��
GE��BD��
��AF=DF��
��AE=EB=$\frac{1}{2}$AB��
��AB=$\sqrt{{AC}^{2}{+BC}^{2}}$=$\sqrt{{8}^{2}{+6}^{2}}$=10��
��AE=$\frac{1}{2}$AB=5��
�ʴ�Ϊ��5��
��3����GE��CBʱ���ı���GAED�����Σ�
��GE��BC��BC��AC��
��GE��AC��
�ɣ�1��֤���ı���GAED��ƽ���ı��Σ�
��?GAED������
��AE=2CD��AD=8-CD��
��AF=$\frac{8-CD}{2}$��
��EF��BC��
��$\frac{AF}{AC}$=$\frac{AE}{AB}$��
��$\frac{\frac{8-CD}{2}}{8}$=$\frac{2CD}{10}$����ã�CD=$\frac{40}{21}$��
��AE=$\frac{80}{21}$��
���� ���⿼����ƽ���ı��ε����ʺ��ж���ȫ�������ε��ж������ʣ����ɶ�����Ӧ�ã����ε��ж���ƽ���ߵȷ��߶ζ�����֪ʶ�㣮


 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ����AOC=��BDO=90�㣬����AOB=150�㣬���DOC�Ķ���Ϊ��������
��ͼ��ʾ����AOC=��BDO=90�㣬����AOB=150�㣬���DOC�Ķ���Ϊ��������| A�� | 30�� | B�� | 40�� | C�� | 50�� | D�� | 60�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪������y=-x2+bx+c����A��3��0����B��2��3�����䶥��ΪM��
��ͼ����֪������y=-x2+bx+c����A��3��0����B��2��3�����䶥��ΪM���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com