
 如图,点A、B、C分别在线段OD、OE、OF上,且AB∥DE,BC∥EF
如图,点A、B、C分别在线段OD、OE、OF上,且AB∥DE,BC∥EF| OA |
| AD |
| OB |
| BE |
| OB |
| BE |
| OC |
| CF |
| OA |
| AD |
| OC |
| CF |
| 6 |
| x |
| x+2 |
| x-0.5 |
| OA |
| AD |
| OB |
| BE |
| OB |
| BE |
| OC |
| CF |
| OA |
| AD |
| OC |
| CF |
| 6 |
| x |
| x+2 |
| x-0.5 |


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
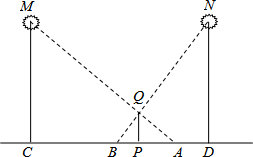 如图所示,某天晚上,身高1.8m的小明站在路灯M和路灯N之间的点P处,发现左右各有两个浅色的影子,其中靠近路灯M的影长BP=0.9m,靠近路灯N的影长PA=1.8m,已知路灯M和路灯N的高度一样,而且两者相距9m,问:路灯M的高度是多少?
如图所示,某天晚上,身高1.8m的小明站在路灯M和路灯N之间的点P处,发现左右各有两个浅色的影子,其中靠近路灯M的影长BP=0.9m,靠近路灯N的影长PA=1.8m,已知路灯M和路灯N的高度一样,而且两者相距9m,问:路灯M的高度是多少?查看答案和解析>>
科目:初中数学 来源: 题型:
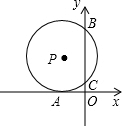 如图,⊙P的圆心在第二象限内,且与x轴相切于点A,与y轴相交于B(0,8)、C(0,2),则圆心P的坐标是( )
如图,⊙P的圆心在第二象限内,且与x轴相切于点A,与y轴相交于B(0,8)、C(0,2),则圆心P的坐标是( )| A、(-3,4) |
| B、(-4,6) |
| C、(-3,5) |
| D、(-4,5) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com