
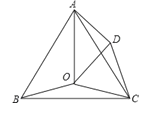
【题目】如图,点O是等边三角形ABC内的一点,∠BOC=150°,将△BOC绕点C按顺时针旋转得到△ADC,连接OD,OA.
(1)求∠ODC的度数;
(2)若OB=4,OC=5,求AO的长.
【答案】(1)60°;(2)![]()
【解析】
(1)根据旋转的性质得到三角形ODC为等边三角形即可求解;
(2)由旋转的性质得:AD=OB=4,结合题意得到∠ADO=90°.则在Rt△AOD中,由勾股定理即可求得AO的长.
(1)由旋转的性质得:CD=CO,∠ACD=∠BCO.
∵∠ACB=∠ACO+∠OCB=60°,
∴∠DCO=∠ACO+∠ACD=∠ACO+∠OCB=60°,
∴△OCD为等边三角形,
∴∠ODC=60°.
(2)由旋转的性质得:AD=OB=4.
∵△OCD为等边三角形,∴OD=OC=5.
∵∠BOC=150°,∠ODC=60°,∴∠ADO=90°.
在Rt△AOD中,由勾股定理得:AO=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
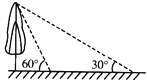
【题目】如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,则树高_____________米(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).
(1)画出△ABC关于点B成中心对称的图形△A1BC1;
(2)以原点O为位似中心,相似比为1∶2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出点C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=kx+2与x轴交于点A(m,0)(m>4),与y轴交于点B,抛物线y2=ax2﹣4ax+c(a<0)经过A,B两点.P为线段AB上一点,过点P作PQ∥y轴交抛物线于点Q.
(1)当m=5时,
①求抛物线的关系式;
②设点P的横坐标为x,用含x的代数式表示PQ的长,并求当x为何值时,PQ=![]() ;
;
(2)若PQ长的最大值为16,试讨论关于x的一元二次方程ax2﹣4ax﹣kx=h的解的个数与h的取值范围的关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
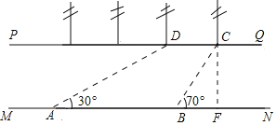
【题目】如图,河流两岸PQ,MN互相平行,C、D是河岸PQ上间隔50m的两个电线杆,某人在河岸MN上的A处测得∠DAB=30°,然后沿河岸走了100m到达B处,测得∠CBF=70°,求河流的宽度(结果精确到个位,![]() =1.73,sin70°=0.94,cos70°=0.34,tan70°=2.75)
=1.73,sin70°=0.94,cos70°=0.34,tan70°=2.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】ABCD中,E是CD边上一点,
(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 ,∠AFB=∠
(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ;
(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是![]()
![]()

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
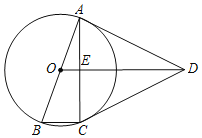
【题目】如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC、OD交于点E.
(1)求证:OD∥BC;
(2)若AC=2BC,求证:DA与⊙O相切.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com