C
分析:由任意选择一对有序整数(b,c),其中每一个整数的绝对值小于或等于5,可得b与c可取的整数分别为:-5,-4,-3,-2,-1,0,1,2,3,4,5共11种情况,然后由乘法公式可求得共有121种等可能的结果;又由方程x
2+bx+c=0没有相异正实根,然后根据判别式与根与系数的关系,即可求得方程x
2+bx+c=0没有相异正实根的情况,继而利用概率公式即可求得答案.
解答:∵任意选择一对有序整数(b,c),其中每一个整数的绝对值小于或等于5,
∴b与c可取的整数分别为:-5,-4,-3,-2,-1,0,1,2,3,4,5共11种情况,
∴有序整数(b,c)共有:11×11=121(种),
∵若方程x
2+bx+c=0有相异正实根,则需:△=b
2-4c>0,-b>0,c>0,
∴方程x
2+bx+c=0有相异正实根的有:(-5,1),(-5,2,),(-5,3),(-5,4),(-5,5),(-4,1),(-4,2),(-4,3),(-3,1),(-3,2)共10种情况,
∴方程x
2+bx+c=0没有相异正实根的情况有:121-10=111(种),
∴方程x
2+bx+c=0没有相异正实根的概率是:

.
故选C.
点评:此题考查了利用乘法公式求概率的知识、根的判别式以及根与系数的关系.此题难度适中,注意掌握概率=所求情况数与总情况数之比.

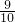
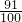

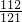
 .
.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案