
分析 根据矩形的性质得出∠ABC=90°,AB=DC,AD=BC,AC=BD,AC=2AO=2CO,BD=2BO=2DO,求出AO=BO=1cm,得出△AOB是等边三角形,推出AB=AO=1cm,在Rt△ABC中,由勾股定理求出BC即可.
解答 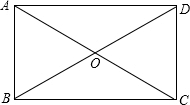 解:如图,∵四边形ABCD是矩形,
解:如图,∵四边形ABCD是矩形,
∴∠ABC=90°,AB=DC,AD=BC,AC=BD,AC=2AO=2CO,BD=2BO=2DO,
∵AC=BD=2cm,
∴AO=BO=1cm,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=AO=1cm,
在Rt△ABC中,由勾股定理得:BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$cm,
即该矩形的较长的边长为$\sqrt{3}$cm.
故答案为:$\sqrt{3}$.
点评 本题考查了矩形性质,等边三角形的性质和判定,勾股定理的应用,注意:矩形的对角线互相平分且相等.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
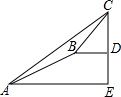 这次数学实践课上,同学进行大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为37°,然后沿在同一剖面的斜坡AB行走5$\sqrt{5}$米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度i=1:2(通常把坡面的垂直高度h和水平宽度l的比叫做坡度,即tanα值(α为斜坡与水平面夹角),那么大树CD的高度约为(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)( )
这次数学实践课上,同学进行大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为37°,然后沿在同一剖面的斜坡AB行走5$\sqrt{5}$米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度i=1:2(通常把坡面的垂直高度h和水平宽度l的比叫做坡度,即tanα值(α为斜坡与水平面夹角),那么大树CD的高度约为(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)( )| A. | 7米 | B. | 7.2米 | C. | 9.7米 | D. | 15.5米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 队名 | 比赛场次 | 胜场 | 负场 | 积分 |
| A | 16 | 12 | 4 | 28 |
| B | 16 | 10 | 6 | 26 |
| C | 16 | 8 | 8 | 24 |
| D | 16 | 0 | 16 | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
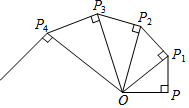 如图OP=1,过P作PP1⊥OP,得$O{P_1}=\sqrt{2}$;再过P1作PP2⊥OP1且PP2=1,得$O{P_2}=\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3=1,得:OP3=2;…依此法继续作下去,得OP2014=$\sqrt{2015}$.
如图OP=1,过P作PP1⊥OP,得$O{P_1}=\sqrt{2}$;再过P1作PP2⊥OP1且PP2=1,得$O{P_2}=\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3=1,得:OP3=2;…依此法继续作下去,得OP2014=$\sqrt{2015}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com