
【题目】如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA、AO,并延长AO交⊙O于点E,与PB的延长线交于点D.
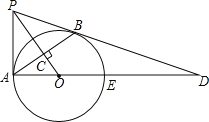
(1)求证:PA是⊙O的切线;(2)若AC=6,OC=4,求PA的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)连接OB,先由等腰三角形的三线合一的性质可得:OP是线段AB的垂直平分线,进而可得:PA=PB,然后证明△PAO≌△PBO,进而可得∠PBO=∠PAO,然后根据切线的性质可得∠PBO=90°,进而可得:∠PAO=90°,进而可证:PA是⊙O的切线;
(2)连接BE,由AC=6,OC=4,可求OA的值,然后根据射影定理可求PC的值,从而可求OP的值,然后根据勾股定理可求AP的值.
(1)证明:如图1,连接OB,则OA=OB,
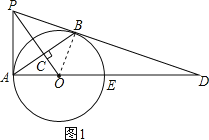
∵OP⊥AB,
∴AC=BC,
∴OP是AB的垂直平分线,
∴PA=PB,
在△PAO和△PBO中,
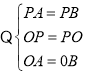 ,
,
∴△PAO≌△PBO(SSS)
∴∠PBO=∠PAO,PB=PA,
∵PB为⊙O的切线,B为切点,
∴∠PBO=90°,
∴∠PAO=90°,
即PA⊥OA,
∴PA是⊙O的切线;
(2)解:如图2,连接BE,
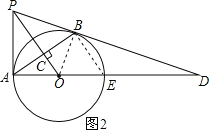
∵OC=4,AC=6,
∴AB=12,
在Rt△ACO中,
由勾股定理得:![]() ,
,
![]() ,
,
在Rt△APO中,
∵AC⊥OP,
∴AC2=OCPC,
解得:PC=9,
∴OP=PC+OC=13,
在Rt△APO中,由勾股定理得:![]() ,
,


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F若平行四边形CDEF的周长是25cm,AC的长为5cm,则![]() 的长是________.
的长是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,已知AB=CD,M、N、P分别是AD、BC、BD的中点∠ABD=20°,∠BDC=70°,则∠NMP的度数为( )
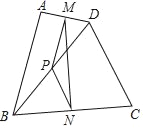
A. 50° B. 25° C. 15° D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
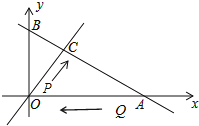
【题目】如图,直线m:y=kx(k>0)与直线n:![]() 相交于点C,点A、B为直线n与坐标轴的交点,∠COA=60°,点P从O点出发沿线段OC向点C匀速运动,速度为每秒1个单位,同时点Q从点A出发沿线段AO向点O匀速运动,速度为每秒2个单位,设运动时间为t秒.
相交于点C,点A、B为直线n与坐标轴的交点,∠COA=60°,点P从O点出发沿线段OC向点C匀速运动,速度为每秒1个单位,同时点Q从点A出发沿线段AO向点O匀速运动,速度为每秒2个单位,设运动时间为t秒.
(1)k= ;
(2)记△POQ的面积为S,求t为何值时S取得最大值;
(3)当△POQ的面积最大时,以PQ为直径的圆与直线n有怎样的位置关系,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
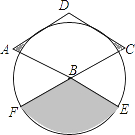
【题目】如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E,F,则图中阴影部分的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到赢利的过程.若该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前七个月的利润总和与t之间的关系)为s=![]() t2-2t.
t2-2t.
(1)第几个月末时,公司亏损最多?为什么?
(2)第几个月末时,公司累积利润可达30万元?
(3)求第8个月公司所获利润是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AD平分∠BAC交⊙O于点D,过点D作DE∥BC交AC的延长线于点E.

(1)试判断DE与⊙O的位置关系,并证明你的结论;
(2)若∠E=60°,⊙O的半径为5,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有4个大小,质地都相同的乒乓球,球面上分别标有数字1,-2,3,-4,小明先从布袋中随机摸出一个球(不放回去),再从剩下的3个球中随机摸出第二个乒乓球.
(1)共有 种可能的结果.
(2)请用画树状图或列表的方法求两次摸出的乒乓球的数字之积为偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y=x+1与y轴交于点A,与双曲线![]() (x>0)交于点B(2,a).
(x>0)交于点B(2,a).
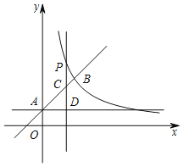
(1)求a,k的值.
(2)点P是直线l上方的双曲线上一点,过点P作平行于y轴的直线,交直线l于点C,过点A作平行于x轴的直线,交直线PC于点D,设点P的横坐标为m.
①若m=![]() ,试判断线段CP与CD的数量关系,并说明理由;②若CP>CD,请结合函数图象,直接写出m的取值范围.
,试判断线段CP与CD的数量关系,并说明理由;②若CP>CD,请结合函数图象,直接写出m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com