
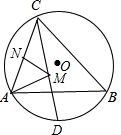
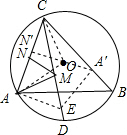
 如图,△ABC内接于半径为2的⊙O,∠ABC=45°,∠ACB=60°,点D为
如图,△ABC内接于半径为2的⊙O,∠ABC=45°,∠ACB=60°,点D为 |
| AB |
| 2 |
| 2 |
| ||
| 2 |
| 6 |
| 6 |
| 2OA2 |
| 2×4 |
| 2 |
 |
| AB |
| 2 |
| 2 |
| ||
| 2 |
| 6 |
| 6 |


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
 如图,一个牧童在小河南4km的A处牧马,此处在也正位于他的小屋B的西12km北5km处,他想把他的马牵到小河边去饮水,然后回家,他要完成这件事情所走的最短路程是多少?
如图,一个牧童在小河南4km的A处牧马,此处在也正位于他的小屋B的西12km北5km处,他想把他的马牵到小河边去饮水,然后回家,他要完成这件事情所走的最短路程是多少?查看答案和解析>>
科目:初中数学 来源: 题型:
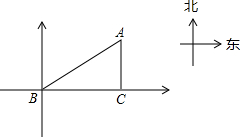 如图,一艘船由西向东航行,上午8时到达B处,看到有一灯塔在它的北偏东60°,距离为72海里的A处,上午10时到达C处,看到灯塔在它的正北方向,则这艘船航行的速度约为( )
如图,一艘船由西向东航行,上午8时到达B处,看到有一灯塔在它的北偏东60°,距离为72海里的A处,上午10时到达C处,看到灯塔在它的正北方向,则这艘船航行的速度约为( )| A、30海里/时 |
| B、31海里/时 |
| C、32海里/时 |
| D、33海里/时 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com