
分析 (1)设每台A型空气净化器的销售利润为a元,每台B型空气净化器的销售利润为b元,根据给定条件“销售10台A型和20台B型空气净化器的利润为4000元,销售20台A型和10台B型空气净化器的利润为3500元”可列出关于a、b的二元一次方程组,解方程组即可得出结论;
(2)①根据购进A型空气净化器的台数,找出购进B型空气净化器的台数,根据A、B间的关系可得出关于x的一元一次不等式,解不等式即可得出x的取值范围,再由销售利润=A型的利润+B型的利润,即可得出y关于x的函数关系式;②结合一次函数的性质以及x的取值范围即可解决最值问题;
(3)该公司要购买A型空气净化器m台,利用净化的体积不少于办公室的体积列不等式$\frac{30}{60}$[340m+240(15-m)]≥600×3.5,然后解方程得到m的范围,在此范围内确定m的最小值即可.
解答 解:(1)设每台A型空气净化器的销售利润为a元,每台B型空气净化器的销售利润为b元,
依题意得:$\left\{\begin{array}{l}{10a+20b=4000}\\{20a+10b=3500}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=100}\\{b=150}\end{array}\right.$.
答:每台A型空气净化器的销售利润为100元,每台B型空气净化器的销售利润为150元.
(2)①设购进A型空气净化器x台,则购进B型空气净化器(100-x)台,
由已知得:100-x≤2x,
解得:x≥$\frac{100}{3}$,
∴x≥34.
∴y=100x+150(100-x)=-50x+15000(x≥34,且x为正整数).
②∵y=-50x+15000中,k=-50<0,
∴y随x的增大而减小,
∴当x=34时,y取最大值,此时100-x=66.
故购进34台A型空气净化器和66台B型空气净化器的销售利润最大.
(3)该公司要购买A型空气净化器m台,
根据题意得$\frac{30}{60}$[340m+240(15-m)]≥600×3.5
解得m≥6,
故该公司至少要购买A型空气净化器6台.
故答案为:6.
点评 本题考查了一次函数的性质以及二元一次方程组的应用,解题的关键是:(1)根据数量关系列出关于a、b的二元一次方程组;(2)根据数量关系列出y关于x的函数关系式;(3)属于一元一次不等式的应用.本题属于中档题,难度不大,解决该题型题目时,根据数量关系列出方程(方程组或函数关系式)是关键.


科目:初中数学 来源: 题型:填空题
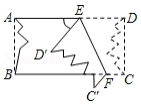 如图,小章利用一张左、右两边已经破损的长方形纸片ABCD做折纸游戏,他将纸片沿EF折叠后,D、C两点分别落在D′、C′的位置,并利用量角器量得∠EFB=66°,则∠AED′等于48度.
如图,小章利用一张左、右两边已经破损的长方形纸片ABCD做折纸游戏,他将纸片沿EF折叠后,D、C两点分别落在D′、C′的位置,并利用量角器量得∠EFB=66°,则∠AED′等于48度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
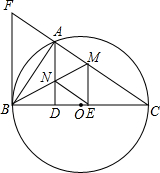 如图,以BC为直径的⊙O交△CFB的边CF于点A,BM平分∠ABC交AC于点M,AD⊥BC于点D,AD交BM于点N,ME⊥BC于点E,AB2=AF•AC.
如图,以BC为直径的⊙O交△CFB的边CF于点A,BM平分∠ABC交AC于点M,AD⊥BC于点D,AD交BM于点N,ME⊥BC于点E,AB2=AF•AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
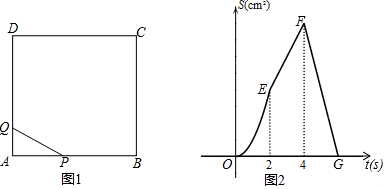
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
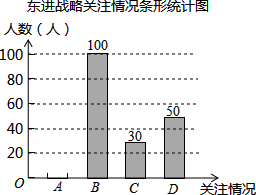 为了解汕头市民对创建文明城市的关注情况,某校数学兴趣小组随机采访部分汕头市民,对采访情况制作了统计图表的一部分如下:
为了解汕头市民对创建文明城市的关注情况,某校数学兴趣小组随机采访部分汕头市民,对采访情况制作了统计图表的一部分如下:| 关注情况 | 频数 | 频率 |
| A.高度关注 | M | 0.1 |
| B.一般关注 | 100 | 0.5 |
| C.不关注 | 30 | N |
| D.不知道 | 50 | 0.25 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com