
【题目】如图,已知一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A,B两点.
的图象交于A,B两点.
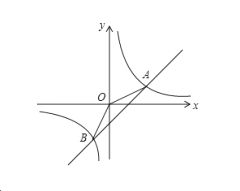
(1)求![]() 的面积;
的面积;
(2)观察图象,可知一次函数值小于反比例函数值的x的取值范围是 .
【答案】(1)4;(2)![]() 或
或![]()
【解析】
(1)首先解一次函数与反比例函数的解析式组成的方程组即可求得A和B的坐标;然后求得AB和x轴的交点,然后根据S△AOB=S△AOC+S△OBC即可求解;
(2)一次函数值小于反比例函数值,即对相同的x的值,一次函数的图象在反比例函数的图象的下边,据此即可求得x的范围.
解:(1)解方程组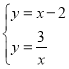 ,
,
即![]() ,解得:x=3或1,
,解得:x=3或1,
则![]() 或
或![]() ,
,
∴A(3,1),B(1,3);
设一次函数![]() 与x轴的交点为C,如下图:
与x轴的交点为C,如下图:
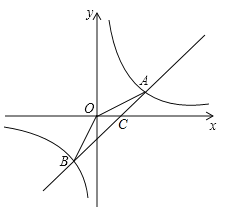
在y=x2中,令y=0,解得:x=2,
则C的坐标是(2,0),则OC=2.
∴S△AOB=S△AOC+S△OBC=![]() ;
;
(2)根据图象所示:当![]() 或
或![]() 时,一次函数图象在反比例函数图象的下边,
时,一次函数图象在反比例函数图象的下边,
此时一次函数值小于反比例函数值,
故答案为:![]() 或
或![]() .
.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】数学活动课上,老师出示了一个问题:
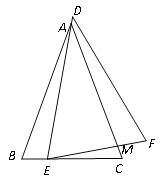
如图,△ABC≌△DEF(点A、B分别与点D、E对应),AB=AC.现将△ABC与△DEF按如图所示的方式叠放在一起,现将△ABC保持不动, △DEF运动,且满足点E在BC边从B向C移动(不与B、C重合),DE始终经过点A,EF与AC边交于点M.求证:△ABE∽△ECM.
(1)请解答老师提出的问题.
(2)受此问题的启发,小明将△DEF绕点E按逆时针旋转, DE、EF分别交线段AB、AC边于点N、M,连接MN,如图2,当EB=EC时,小明猜想△NEM与△ECM相似.小明的猜想正确吗?请你作出判断,并说明理由.
(3)在(2)的条件下,以E为圆心,作⊙E,使得AB与⊙E相切,请在图3中画出⊙E,并判断直线MN与⊙E的位置关系,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C、D在⊙O上,AD与BC相交于点E.连接BD,作∠BDF=∠BAD,DF与AB的延长线相交于点F.
(1)求证:DF是⊙O的切线;
(2)若DF∥BC,求证:AD平分∠BAC;
(3)在(2)的条件下,若AB=10,BD=6,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在初中阶段的函数学习中,我们经历了“确定函数的表达式——利用函数图象研究其性质一一运用函数解决问题"的学习过程.在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.同时,我们也学习了绝对值的意义![]() .结合上面经历的学习过程,现在来解决下面的问题在函数
.结合上面经历的学习过程,现在来解决下面的问题在函数![]() 中,当
中,当![]() 时,
时,![]() 当
当![]() 时,
时,![]()
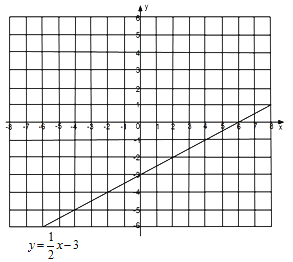
(1)求这个函数的表达式;
(2)在给出的平面直角坐标系中,请用你喜欢的方法画出这个函数的图象井并写出这个函数的一条性质;
(3)已知函![]() 的图象如图所示,结合你所画的函数图象,直接写出不等式
的图象如图所示,结合你所画的函数图象,直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在平面直角坐标系中,直线AB分别与x轴、y轴交于A、B两点(OA<OB),且OA、OB的长分别是一元二次方程x2-18x+72=0的两根,点D为线段OB的中点,过点D作AB的垂线与线段AB相交于点C.
(1)求A、B两点的坐标;
(2)求过点C的反比例函数解析式;
(3)已知点P在直线AD上,在平面内是否存在点Q,使以A、O、P、Q为顶点的四边形为菱形?若存在,请直接写出点Q坐标;若不存在,请说明理由.
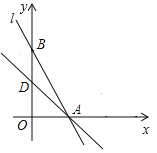
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系xOy中点A的坐标为(﹣1,1),点B的坐标为(3,3),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点E.
(1)求点E的坐标;
(2)求抛物线的函数解析式;
(3)点F为线段OB上的一个动点(不与点O、B重合),直线EF与抛物线交于M、N两点(点N在y轴右侧),连接ON、BN,当四边形ABNO的面积最大时,求点N的坐标并求出四边形ABNO面积的最大值.
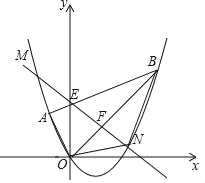
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年2月16日,由著名导演林超贤的电影《红海行动》在各大影院上映后,好评不断,小亮和小丽都想去观看这部电影,但是只有一张电影票,于是他们决定采用摸球的办法决定谁去看电影,规则如下:在一个不透明的袋子中装有编号1~4的四个球(除编号外都相同),从中随机摸出一个球,记下数字后放回,再从中摸出一个球,记下数字,若两次数字之和大于5,则小亮获胜,若两次数字之和小于5,则小丽获胜.
(1)请用列表或画树状图的方法表示出两数和的所有可能的结果;
(2)分别求出小亮和小丽获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象交
的图象交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,点
,点![]() 在线段
在线段![]() 上(不与点
上(不与点![]() ,
,![]() 重合)过点
重合)过点![]() 分別作
分別作![]() 和
和![]() 的垂线,垂足为
的垂线,垂足为![]() ,
,![]() .
.

(1)关于矩形![]() 面积的探究:
面积的探究:
①点![]() 在何处时,矩形
在何处时,矩形![]() 的面积为1?写出计算过程;
的面积为1?写出计算过程;
②是否存在一点![]() ,能使矩形
,能使矩形![]() 的面积为
的面积为![]() ?说说你的理由.
?说说你的理由.
(2)设点![]() 的坐标是
的坐标是![]() ,
,![]() ,图中阴影部分的面积为
,图中阴影部分的面积为![]() ,尝试完成下列问题:
,尝试完成下列问题:
①建立![]() 与
与![]() 的关系式,并类比一次函数猜想
的关系式,并类比一次函数猜想![]() 是
是![]() 的什么函数,能否对此类函数下一个描述性的定义,其中包含它的一般形式;
的什么函数,能否对此类函数下一个描述性的定义,其中包含它的一般形式;
②我们知道代数式![]() 有最小值9,试问当
有最小值9,试问当![]() 在何处时
在何处时![]() 有最小值,请把你的理由.
有最小值,请把你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=﹣x+4与反比例函数![]() 的图象相交于点A(﹣2,a),并且与x轴相交于点B.
的图象相交于点A(﹣2,a),并且与x轴相交于点B.
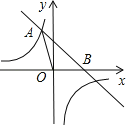
(1)求a的值;
(2)求反比例函数的表达式;
(3)求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com