
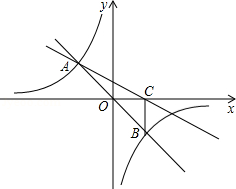
【题目】如图,在直角坐标系xOy中,直线y=mx与双曲线 ![]() 相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1. 
(1)求m、n的值;
(2)求直线AC的解析式.
【答案】
(1)解:∵直线y=mx与双曲线y= ![]() 相交于A(﹣1,a)、B两点,
相交于A(﹣1,a)、B两点,
∴B点横坐标为1,即C(1,0),
∵△AOC的面积为1,
∴A(﹣1,2),
将A(﹣1,2)代入y=mx,y= ![]() 可得m=﹣2,n=﹣2;
可得m=﹣2,n=﹣2;
(2)解:设直线AC的解析式为y=kx+b,
∵y=kx+b经过点A(﹣1,2)、C(1,0)
∴ ![]() ,
,
解得k=﹣1,b=1,
∴直线AC的解析式为y=﹣x+1.
【解析】(1)由题意,根据对称性得到B的横坐标为1,确定出C的坐标,根据三角形AOC的面积求出A的纵坐标,确定出A坐标,将A坐标代入一次函数与反比例函数解析式,即可求出m与n的值;(2)设直线AC解析式为y=kx+b,将A与C坐标代入求出k与b的值,即可确定出直线AC的解析式.


科目:初中数学 来源: 题型:
【题目】如图,将边长为4的正方形ABCD的一边BC与直角边分别是2和4的Rt△GEF的一边GF重合.正方形ABCD以每秒1个单位长度的速度沿GE向右匀速运动,当点A和点E重合时正方形停止运动.设正方形的运动时间为t秒,正方形ABCD与Rt△GEF重叠部分面积为S,则S关于t的函数图象为( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOC=30°,∠BOC=150°,OD为∠BOA的平分线,则∠DOC=90°.若A点可表示为(2,30°),B点可表示为(4,150°),则D点可表示为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在ABCD中,分别以AB,AD为边分别向外作等边三角形ABE和等边三角形ADF,延长CB交AE于点G,点G在点A,E之间,连接CE,CF,EF,则下列结论不一定正确的是( )

A. △CDF≌△EBC B. ∠CDF=∠EAF
C. △ECF是等边三角形 D. CG⊥AE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一工程,在工程招标时,接到甲、乙两个工程队的投标书.甲工程队施工一天,需付工程款1万元;乙工程队施工一天,需付工程款0.6万元.根据甲、乙工程队的投标书测算,可有三种施工方案:
(A)甲队单独完成这项工程,刚好如期完成;
(B)乙队单独完成这项工程要比规定工期多用4天;
(C)若甲、乙两队合做3天后,剩下的工程由乙队单独做,也正好如期完工.
为了节省工程款,同时又能如期完工,你认为应选择哪一种方案?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC.
(1)请按如下步骤用直尺和圆规作图(保留作图痕迹并在图中标注字母):
①作∠ABC的平分线交AC边于点D;
②在BC的延长线上截取CE=CD;
③连接DE.
(2)求证:BD=DE.
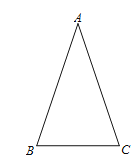
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、E分别在直线AC和DF上,若∠AGB=∠EHF,∠C=∠D,可以证明∠A=∠F.请完成下面证明过程中的各项“填空”.

证明:∵∠AGB=∠EHF(理由: )
∠AGB= (对顶角相等)
∴∠EHF=∠DGF,∴DB∥EC(理由: )
∴ =∠DBA(两直线平行,同位角相等)
又∵∠C=∠D,∴∠DBA=∠D,
∴DF∥ (内错角相等,两直线平行)
∴∠A=∠F(理由: ).
查看答案和解析>>
科目:初中数学 来源: 题型:
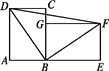
【题目】如图,把长方形ABCD旋转到长方形GBEF的位置,此时点A,B,E在一条直线上.
(1)指出这个过程中的旋转中心,并说明旋转角度数是多少;
(2)指出图中的对应线段;
(3)连接BD,BF,DF,判断△DBF的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com