
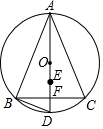
 如图,在△ABC中,AB=AC,AD⊥BC于点F,交△ABC外接圆于点D,BC=6,tan∠BAC=$\frac{3}{4}$,点E是△ABC内切圆的圆心,则OE的长为5-$\sqrt{10}$.
如图,在△ABC中,AB=AC,AD⊥BC于点F,交△ABC外接圆于点D,BC=6,tan∠BAC=$\frac{3}{4}$,点E是△ABC内切圆的圆心,则OE的长为5-$\sqrt{10}$. 分析 连接BE.依据三角形的内心的性质以及圆周角定理证明∠DBE=∠DEB,得出BD=DE;连接OB.先证明圆周角定理和三角形的内心的性质可知∠BAC=∠BOF,依据锐角三角函数的定义可求得OB的长,然后依据勾股定理可求得OF的长于是得到DF的长,在△BDF中,由勾股定理可求得BD的长,依据问题(1)的结论可得到DE的长,从而求得OE的长.
解答 解:连接BE、OB.如图所示: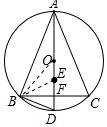
∵是△ABC的内心,
∴∠ABE=∠CBE,∠BAD=∠CAD.
∵∠DBC=∠CAD.
∴∠DBC=∠BAD.
∵∠BED=∠BAD+∠ABE,
∴∠DBE=∠DEB.
∴BD=ED.
∵AD⊥BC,
∴BD=FC=3.
∵∠BAC=∠BOD,tan∠BAC=$\frac{3}{4}$,BF=3,
∴OF=4,
∴OB=5,
∴DF=1.
在Rt△BDF中,BF2+DF2=BD2.
∴BD=$\sqrt{10}$.
∴DE=$\sqrt{10}$.
∴OE=5-$\sqrt{10}$;
故答案为:5-$\sqrt{10}$.
点评 本题主要考查的是三角形的内心的性质、勾股定理的应用、圆周角定理、锐角三角函数的定义,依据锐角三角函数的定义求得OB的长度是解题的关键.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
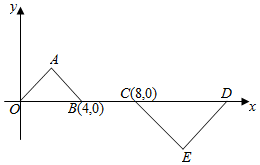 如图所示,等腰直角三角形OAB和等腰直角三角形CDE是位似图形,点A的坐标为(2,2),点E的坐标为(12,-4),则这两个等腰直角三角形的位似中心的坐标为($\frac{16}{3}$,0).
如图所示,等腰直角三角形OAB和等腰直角三角形CDE是位似图形,点A的坐标为(2,2),点E的坐标为(12,-4),则这两个等腰直角三角形的位似中心的坐标为($\frac{16}{3}$,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD中,E为AB的中点.DF⊥CE.若AD=8.AB=4.则CF=$\frac{4\sqrt{17}}{17}$,DF=$\frac{16\sqrt{17}}{17}$.
如图,矩形ABCD中,E为AB的中点.DF⊥CE.若AD=8.AB=4.则CF=$\frac{4\sqrt{17}}{17}$,DF=$\frac{16\sqrt{17}}{17}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
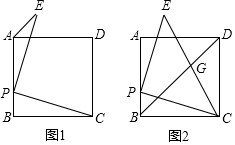
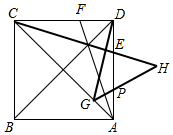 在正方形ABCD中,DE=DF,DG⊥CE,交CA于G,GH⊥AF,交AD于P,交CE延长线于H,请问三条粗线DG,GH,CH的数量关系.
在正方形ABCD中,DE=DF,DG⊥CE,交CA于G,GH⊥AF,交AD于P,交CE延长线于H,请问三条粗线DG,GH,CH的数量关系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com