

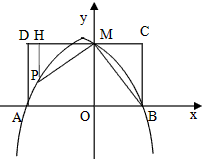
| 解(1)∵MO=MD=4,MC=3, ∴M、A、B的坐标分别为(0,4),(-4,0),(3,0) 设BM的解析式为y=kx+b, 则 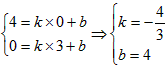 , ,∴BM的解析式为 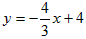 ; ;(2)设抛物线的解析式为 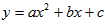 , ,则 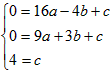 ,解得a=b=- ,解得a=b=-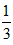 ,c=4, ,c=4,∴ 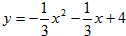 ; ;(3)设抛物线上存在点P,使△PMB构成直角三角形。 分别过M、B作MB的垂线,它与抛物线的交点即为P点。 过M作MB的垂线与抛物线交于P,过P作PH⊥DC交于H, ∴∠PMB=90°, ∴∠PMH=∠MBC, ∴△MPH∽△BMC, ∴PH∶HM=CM∶CB=3∶4, 设HM=4a(a>0),则PH=3a, ∴P点的坐标为(-4a,4-3a), 将P点的坐标代入 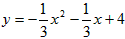 得: 得: , ,解得a=0(舍去), 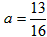 , ,∴P点的坐标为 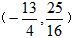 。 。 |
 |


科目:初中数学 来源: 题型:
 |
| BDC |
 的延长线分别交于点F、E,且
的延长线分别交于点F、E,且 |
| BF |
 |
| AD |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com